四、结果与讨论

压力面积等温线是通过压缩获得 在朗缪尔槽上涂抹单层膜，用于 3 组不同的 实验。 这些等温线中的区域坐标被缩放 由吸附在界面上的颗粒数量决定。 一切 曲线折叠成单个图，如图 1 所示。 增加压缩，压力最初变化很小，但 每个颗粒低于 2 mm2，压力会急剧增加。 曲线的斜率首先增加，但达到 最大在 ~27 mN m- 1 处有一个拐点 其次是稍弱的斜率。 面积值 对应于该拐点的粒子 (Ac) 结果为 为 0.545 mm2，如图 1 中的虚线所示。假设 颗粒紧密堆积，这对应于~835 nm 的颗粒间距离，远大于 在本体中测量的颗粒的流体动力学直径 溶液 (590 nm) 表明颗粒确实是 大幅度变形。 如图 1 的插图所示，有限 0.5 mN m- 1 级的表面压力（即远高于我们的 检测限为 0.1 mN m- 1 ) 事实上已经可以测量了 每个粒子的面积约为 4 mm2 . 插图还表明 P 的绝对值可再现在 0.3 mN m- 1 以内 在两个不同朗缪尔的不同实验之间 槽。

在图 2 中，我们展示了与图 1 相同的数据，但转换了 使用 G ¼ 1/(A * NAv) 绘制压力与吸附量曲线 其中 A 是图 1 中每个粒子的面积，NAv 是阿伏伽德罗数。 这条曲线代表了二维状态方程 (EOS) 本系统。 在相对较低的密度 (<5 * 10- 13 摩尔米- 2 ) 压力极低 (z1 mN m- 1 ） 但 相当好检测。 因此，即使在低密度下， 粒子间距离远大于溶液中的粒子大小，粒子仍然以某种方式相互作用。 作为粒子 几乎没有任何电泳迁移率，22,23 静电 排斥不太可能是原因。 唯一的其他选择是 颗粒-颗粒接触。 因此粒子必须强 吸附在界面上时发生变形，即 定性地同意其他作者的发现。2,3,7,8,15,24 我们可以粗略估计变形的程度 ansatz Dr z Dg/3。 使用 3 z 50 kPa 的典型值 文献 25,26 以及 Dg ¼ 70 mN m- 1 , 我们发现 ¼ 博士 1.7 毫米，与约 3 毫米之间的距离一致 密堆积和完全变形的颗粒。 我们基于我们的分析 假设我们传播的粒子 界面不解吸。 但即使我们考虑了解吸 粒子，这只会意味着有限的压力 检测到的实际上对应于更低的表面 浓度。 图3显示了界面处颗粒变形机制的示意图。 它 应该注意的是，在 LB 实验的情况下，粒子是 散布在界面上，我们没有任何粒子 大部分。 在界面张力测量的情况下， 粒子从本体扩散到界面。

图 1 PNIPAM 颗粒在空气-水中的压力面积等温线 界面。 空心符号表示对应于三组不同实验的实验数据点，即： (,) NIMA 具有高初始颗粒负载的槽，(B) 具有低初始颗粒负载的 NIMA 槽 初始粒子负载和 (D) Kibron m-trough 具有高初始粒子 加载。 插图显示了低压力区域曲线的扩展视图 负荷。 插图中的虚线表示检测限 压力传感器。

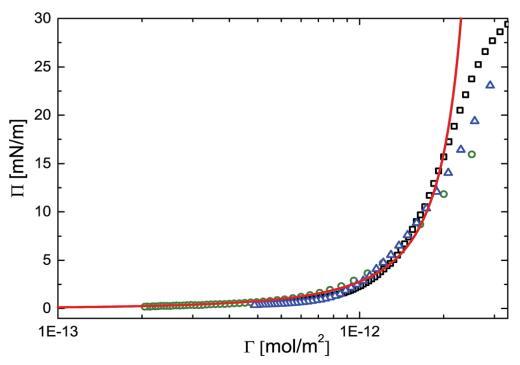
图 2 表面压力（P）与吸附的 PNIPAM 颗粒量 (G) 在空气-水界面上。 开放符号表示实验 对应于三组不同实验的数据点 即：（，）具有高初始粒子负载的 NIMA 槽，（B）NIMA 低初始粒子负载的槽和 (D) Kibron m 槽 高初始粒子负载。 红色实线表示预测 使用 Groot 和 Stoyanov 模型制作。

吸附在流体-流体界面上的粒子与 并产生表面压力 (P)，即 3D 系统中压力的 2D 模拟。 通过扩展这个 进一步类比，也可以将这个表面压力联系起来 通过状态方程到其他状态参数，如数密度和温度。 用于吸附胶体颗粒 在流体-流体界面上，最简单的近似可能是 2D硬盘。 状态方程 (EOS) 为一个 组件系统根据密度相关性给出 压缩系数 Z。文献中充满了 提供表达的多种方法 EOS 2D 硬盘液。 Mulero 等人 27,28 提供了一个简洁的 回顾和比较所有这些状态方程。

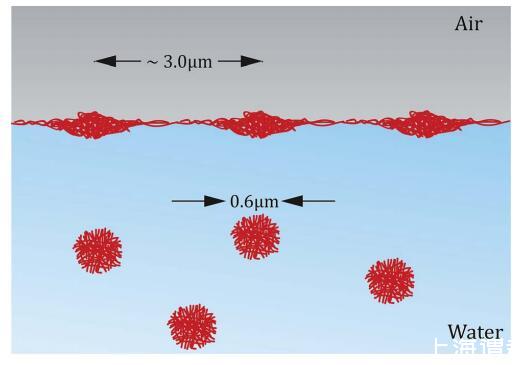
图3 微凝胶变形示意图 颗粒在非常低的负载下吸附到界面上 状况。

我们发现在非常低的密度下，表面压力 测量值至少高出 5-6 个数量级 假设在这些密度下是非相互作用粒子的理想气体，对表面压力的预测。 Groot 和 Stoyanov13 做 由于没有明确考虑这些粒子的变形 表面张力。 他们只是假设压力 主要取决于胶体颗粒内聚合物的微观结构和组成，并引入 新的长度尺度 deff 旨在反映颗粒微观结构，并将压力放大到实验 值。 然而，意识到粒子扩散到一个大 在某种程度上，我们还可以看到测量的压力反映了 颗粒的内部弹性。 由于这是由 2D 给出的 交联的密度，我们发现微观长度也就不足为奇了。

Groot 和 Stoyanov 提出了表面压力 (P) 的表达式，该表达式考虑了粒子内这些较小相关域的大小，由下式给出：

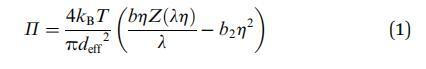
其中，diff 是相关域的大小 粒子。 压缩系数 (Z) 可以表示为 使用文献中可用的任何状态方程。 在我们的 在这种情况下，我们使用修改后的亨德森方程 29 给出：

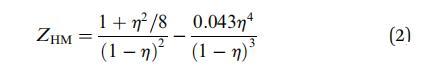
其中 h 是表面堆积分数，它可以反过来 用粒子数密度 (r) 和 单个颗粒的体积直径 (d) 作为 h ¼ (p/4)rd2 . 对于我们的 实验中，h 介于 0 和 0.91 之间。 相应的 ZHM 的值介于 1 到 96 之间。 我们将 Groot 和 Stoyanov 给出的比例关系拟合到我们的 图2中的数据（红色曲线）。 拟合给出了 deff ¼ 1.25 nm 作为 特征长度尺度。 为了提供实物图片，这 deff 可以看作是交联之间的平均距离 微凝胶颗粒内。 这与之前的一致 研究 30,31 报告了 1-10 nm 范围内的网格尺寸。 模型中使用的参数 b 和 l 表示由于圆盘的弹性性质而产生的排斥相互作用。 对于我们的系统， b 和 l 的值可以统一。13 参数 b2 表示短程有吸引力的相互作用。 我们检查了 通过结合短距离吸引相互作用的影响 参数 b2 作为拟合参数，但分析产生极 b2 的小值（~1 * 10-4 次方）。 因此我们得出结论，我们有 纯排斥粒子。 与实际数据的偏差 高负载的模型可能是因为在高 压缩，表面不再保持平坦，而是经历 平面外变形，即弯曲。 还有这些颗粒 有很多松散的、未交联的聚合物链段 沿着这些粒子的外围。 在高压缩时，它 积极地有利于这些细分市场离开 接口而不是相互渗透。 这种部分解吸 也可能导致与硬盘预测的偏差 喜欢模型。

已经建立了一个状态方程来关联 表面压力和吸附量，我们现在继续 研究颗粒的吸附动力学。 为此我们 监测新鲜的界面张力的演变 在 PNIPAM 颗粒悬浮液中制备气泡作为 时间的函数。 我们转换界面张力值 转化为表面压力。 结果如图 4 所示。 表面压力值最初迅速增加，然后 放松到最终的平衡值。 动态可以一目了然 分为两个独立的时间尺度：初始快速 由表面压力增加表示的动力学 值，以及随着系统向最终放松而缓慢的部分 平衡状态。 快速动力学之间的这种区别 短时间和长时间慢得多的动力学是许多表面活性物质的吸附行为的特征 材料.32,33

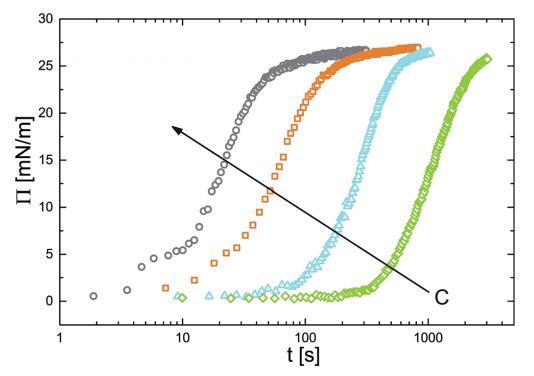
图 4 表面压力 (P) 随时间的演变。 这 空心符号是实验数据点。 不同的符号和 颜色表示颗粒的各种体积浓度：(>)0.10 g l-1 ，（四） 0.20 克 l-1 , (,)0.50 克 l- 1 , (B)1.00 克 l-1 . 箭头表示方向 增加浓度。

在短时间尺度上，P 的增加受到 颗粒从主体到界面的传输。 我们 预计传输受粒子扩散控制。 由于我们的粒子相当大，吸附能为 这些粒子比 kBT 高 3-4 个数量级。 因此可以安全地假设粒子永远不会离开 吸附后的界面。 在这些条件下， Ward 和 Tordai 模型 34 给出：

其中，G 是吸附摩尔质量，C 是体积浓度，D 是颗粒的扩散系数。

使用图 2 中获得的实验 P 与 G 曲线，我们 将 P(t) 数据转换为 G(t) 数据，然后将 G 与 Ct1/2 绘制为 如图 5 所示。我们用浓度缩放时间轴 期望曲线折叠成一条曲线。 我们什么 观察到 G 的初始增长遵循 t 1/2 依赖性很好。 其次是浓度依赖性 随着系统长时间放慢 G 的弛豫 接近饱和。 图 5 中的插图显示了个体 不同颗粒浓度的 G 与 t1/2 曲线。 这 实线是拟合实验数据初始部分的直线（空心符号）。 每条曲线的初始斜率 产生扩散系数 D 的值。为了比较， 虚线是用 D 计算的斜率绘制的 从动态光散射 (DLS) (DDLS ¼ 7.29 * 10- 13 平方米 s- 1 ）。 可以看出，它们的偏差不大 从实验曲线。 或者，我们可以确定 D 从最佳拟合到数据。 表 1 给出了 D 的值 通过将直线（实线）拟合到不同体积浓度的实验结果并比较 从 DLS 获得的值。 如此获得的值做 与 DLS 测量值的偏差不超过 10%。

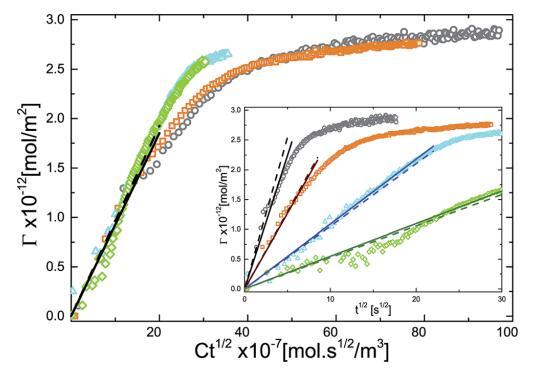
图 5 吸附量 (G) 作为乘积 Ct1/2 的函数。 这 插图显示了不同体积的 G 与 t1/2 的单独曲线 微凝胶颗粒浓度：(>)0.10 g l-1 , (D)0.20 克 l-1 , (,) 0.50 克 l-1 , (B)1.00 克 l-1 . 实线是直线拟合和虚线 用使用 D ¼ DDLS 计算的斜率绘制。

表 1 扩散系数 D (m2 s- 1 ) 对于各种 从实验 G vs. t1/2 曲线计算的浓度 与使用 DLS 测量的相比

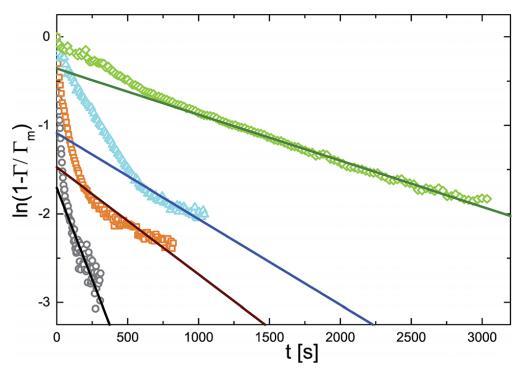
图 6 ln(1 - r/rm) 作为不同体积浓度的时间函数 微凝胶颗粒：(>)0.10 g l-1 , (D)0.20 克 l-1 , (,)0.50 克 l- 1 , (乙) 1.00 克 l- 1 . 实线是直线拟合。

表 2 不同浓度的速率常数 k(1/s) 值 由图 6 中的实验曲线计算

当系统接近饱和时，G(t) 的下降必须 随着表面变得拥挤，请减速。 的浓度 吸附在表面下方，然后失去平衡 与吸附的物种和动力学受到限制 吸附屏障。 然后一级动力学过程导致：

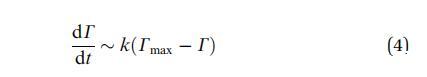
其中，k 是与吸附有关的速率常数 障碍。 理想情况下，k 应该与局部溶质成正比 界面下方的浓度。 这导致指数 松弛：

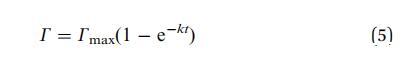
图 6 表明，这种屏障控制机制确实 确实存在很久了。 空心符号是 ln(1 - G/Gmax) 的实验值。 在很长一段时间内，曲线拟合一个 用实线表示的直线。 的斜坡 实线可以识别为动力学松弛的倒数 时间为 1/k。

如表 2 所示，速率常数取决于体积 微凝胶颗粒的浓度。 但是依赖是 不是线性的。 这可能表明吸附 过程本身相当复杂，取决于细节 界面上粒子的构型。 更深入的分析 这些方面超出了当前工作的范围。

微凝胶颗粒在气液界面处吸附动力学及动态方程研究——摘要、简介

微凝胶颗粒在气液界面处吸附动力学及动态方程研究——材料与方法

微凝胶颗粒在气液界面处吸附动力学及动态方程研究——结果与讨论

微凝胶颗粒在气液界面处吸附动力学及动态方程研究——结论、参考！