挤出成型因为具有实用范围广、生产效率高、投资少、见效快等一系列优点而成为高聚物成型的最重要的方法之一。近年来，产品微型化呈现出蓬勃发展的趋势。挤出产品也朝着微型化的方向发展。由于微尺度效应的影响，宏观的工艺参数、结构参数、物理参数不能简单的按几何比例缩小应用到微挤出成型过程中。一些在宏观挤出中可以忽略的影响因素包括壁面滑移、表面张力、对流换热、黏性耗散等在微尺度效应下变得不可忽略，甚至成为影响微挤出成型的主要因素。对塑料熔体在微型通道内的流变行为的研究是对流变理论的一种完善和补充，有助于推动微挤出的不断完善，并且有利于扩大塑料微挤出技术的应用领域。

本文采用Polyflow软件对聚合物在微通道中的流变行为进行数值模拟，研究了表面张力对微挤出流场的影响。

1表面张力

1.1定义或解释

促使液体表面收缩的力叫做表面张力，其本质是分子力，是液体表面层由于分子引力不均衡而产生的沿表面作用于任一界线上的张力。表面张力的方向和液面相切，其合力沿着曲面法向方向。接触角用来表示表面张力的方向。表面张力及接触角如图1所示。

单位面积上的表面张力的合力fn使表面曲率减少，σ为表面张力系数，满足式（1）：

图1表面张力及接触角

式中fn——单位面积上的法向力，N／m2

σ——表面张力系数，N／m

R——材料接触界面的高斯曲率，m

n——液体自由表面法向方向的单位矢量

R满足式（2）：

式中R1、R2——接触界面的2种材料的曲率半径

表面张力的方向和液面相切，液体表面由于表面张力作用所引起的切向力为：

式中fτ——液体表面上受到的切向力

l——自由表面的长度

τ——液体自由表面切向方向的单位矢量

通常用接触角（θ）来描述切向力的方向。以水平线为参考线，逆时针为正，顺时针为负：

在计算流体力学中，常采用Brackbill的连续表面力模型CSF 将界面的表面张力项离散为等效的体积力，以附加体积力的方式加到流体的动量方程中。它分布在交界面上很薄的一层区域内。其离散公式为：

式中k——界面上的曲率

δ（x）——界面上的函数

n——界面上的法向向量（向外为正）

δ（x-xs）——狄拉克δ函数

xs——界面S上的点

2数值模拟

采用聚合物专用流体分析软件Polyflow，对圆形截面的流道进行模拟分析，探讨表面张力的尺寸效应及表面张力系数和接触角对微挤出流场的影响。由于流道结构及流场的对称性，本模拟采用轴对称分析。模拟分析的流道尺寸及网格划分如图2所示。微通道尺寸AE＝4×AB＝1.2mm。网格采用四边形结构单元。节点数量为3751，网格数量为3600。

图2微通道的网格

在数值模拟时，熔体自由表面在模拟的过程中会发生变形，自由表面的网格会因为自由表面位置的变化而发生变化。此时，需要采用网格重置技术。网格重置可以根据边界点的位置的变化重新定位内部网格节点。Spine法是一种比较简单，适用于二维挤出成型的网格重置方法。其网格节点是沿着线性进行重新组织的，如图3所示。节点的位置确定是按照一维方式进行逻辑排列的，这就像是对二维平面进行切片，切片的方式是沿着自由表面或者移动边界的法向方向，从而得到最终的网格。Spine法是线性组织的，并且在每个线段的端点处都有相应的节点。假设x1、x2是线段的2个端点。按照Spine法的规则，内部节点的位移数学表达式为：

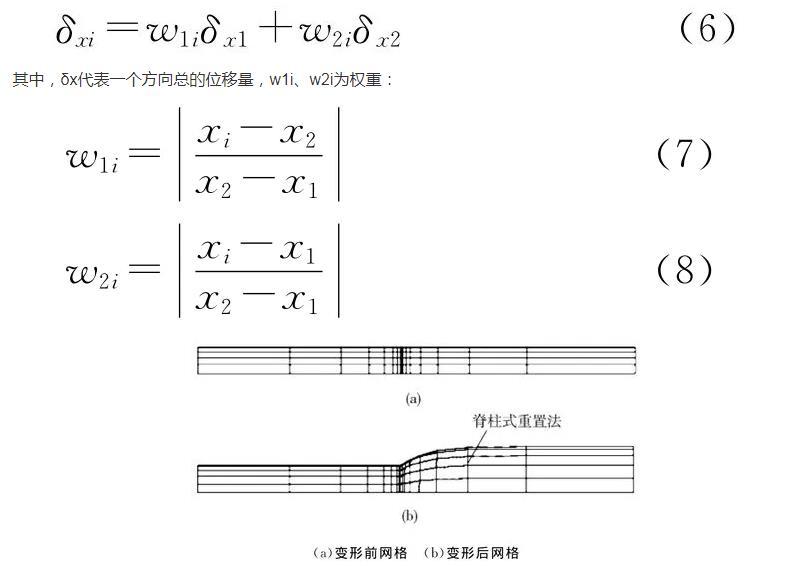
图3 Spine法变形网格

塑料熔体的表面张力系数一般在50N／mm左右，模拟时表面张力系数的取值范围为（0～50N／mm），接触角取值范围为（-50°～50°）。材料黏度模型采用常数η0＝100Pa·s。边界条件设定为：EF为材料进口端，法向速度设置为10mm／s，BF为对称轴，CE壁面处的速度为零，AB边界设置为法向力等于零，切向力等于零，AC为自由表面。