3变形液滴曳力系数模型

假设液滴体积不变，只在外力作用下液滴表面积发生变化，且液滴不与其他液滴合并，液滴本身也不发生分裂。则液滴会在压差作用下由球形变成椭球形。

如图4所示，ds为球形液滴的直径，m；d为液滴变形后迎风面直径，m；h为椭球体短轴高度，m。液滴等效直径比φ为球形液滴直径与变形后迎风面直径比，即φ=ds/d。当液滴为椭球形时，其表面积近似为

液滴变形前后体积不变，即ds3=d2h，则液滴变形程度系数为

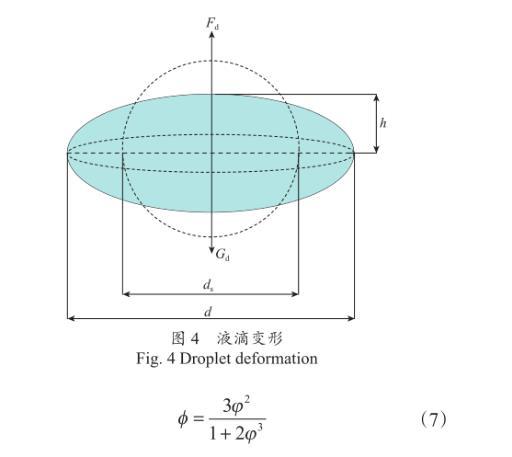
图4液滴变形

式中，φ为液滴变形程度系数，为与变形液滴体积相等的等效球形表面积与实际液滴表面积的比值。当气液相对速度不大时，液滴保持球形，可以利用球形液滴曳力系数计算携液临界流量，但是当液滴发生变形以后，曳力系数和液滴迎风面积相应的发生改变，用球形液滴曳力系数计算误差可能高达30%，对于非球形刚性颗粒，可以应用如下曳力系数表达式进行计算：

式中，μg为气体动力黏度，Pa·s。从式（8）可知，曳力系数与液滴大小有关。液滴为了保持液滴形状不产生分裂，最大液滴韦伯数的范围为20～30，可以表述为

式中，Nw为球形液滴韦伯数；dmax为球形液滴最大直径，m。

根据Turner模型可以得到球形液滴最大直径为

4、考虑液滴尺寸和变形影响的携液临界模型

气体携液满足的基础力学条件为向上曳力等于液滴重力，即假设液滴在气流中受到前后压差作用，发生变形，变形前后体积不变，则液滴体积和投影面积为

式中，Vd为液滴为球形时的体积，m3。

考虑到携带液滴直径d=dmax时，联立式（14）、（16）、（17）、（18）得到携液临界流速为

式中，vcr为携液临界流速，m/s。模型中液滴等效直径比反映了液滴的变形程度，而变形程度又与液滴尺寸有关，Shi Juntai于2014年给出了液滴厚度（图4中h）与长度（图4中d）之间的关系

式中，α为液滴厚度与长度之比。

根据式（6）和式（20），可以得到最大液滴等效直径比为

联立界面张力公式（式4）、变形系数公式（式7）、曳力系数公式（式8）、韦伯数公式（式14），携液临界流速公式（式19）、等效直径比公式（式21），若液滴尺寸未知，还需结合最大液滴公式（式15），假设携液临界流量和曳力系数初始值分别为Turner模型和0.44，通过方程组隐式迭代求解得到曳力系数和携液临界流量。最后得到气井携液临界流量为

式中，qcr为携液临界流量，m3/d；Aw为井筒横截面面积，m2；p为井筒压力，MPa；Z为偏差因子；T为温度，K。

5、参数敏感性分析

（1）界面张力对携液临界流量影响。如图5所示为气体相对密度为0.7，温度为100℃时，利用新模型计算当界面张力为常数（60 mN/m）和界面张力随压力变化时不同压力下的携液临界流速。考虑界面张力变化的携液临界流速要比界面张力为常数时的小，计算精度更高。且随着压力的增大，携液临界流速的计算精度提高百分比，逐渐从4%上升至12.5%，平均提高了8%。

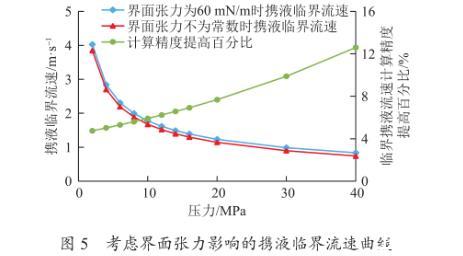
图5考虑界面张力影响的携液临界流速曲线

（2）液滴尺寸和液滴变形。如图6所示为压力15 MPa，温度50℃时不同液滴尺寸下液滴变形程度、曳力系数的变化趋势。从中可知，当液滴特别小时（1 mm），等效直径比及变形程度系数接近1，曳力系数近似0.44，液滴呈球形基本不发生变形；随着液滴尺寸从1 mm增大到10 mm时，等效直径比从1减小到0.75，变形程度系数从1减小到0.45，曳力系数从0.44增大到4.3，液滴呈椭球形变形程度逐渐加大。

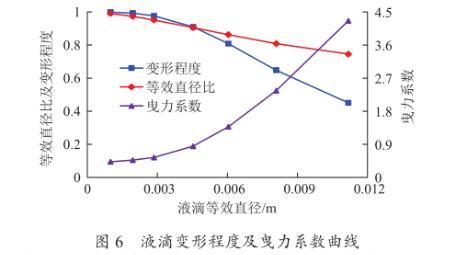
图6液滴变形程度及曳力系数曲线

如图7所示为不同液滴直径下携液临界流速。从中可知，当液滴特别小时（约为1 mm），液滴形变不明显，所得到的模型与Turner模型相同；随着液滴变大，液滴变形严重，曳力系数增大，携液临界流速变小。在一定液滴大小及形状下，模型简化为常用的携液临界流量模型，例如李闽模型对应的液滴尺寸为8 mm，等效直径比为0.8，液滴变形程度系数为0.65。

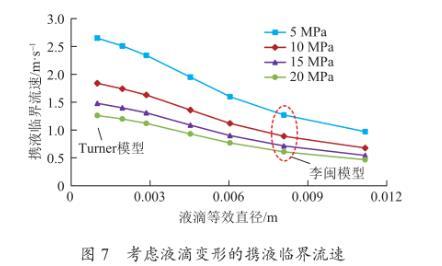
图7考虑液滴变形的携液临界流速

6、模型验证

利用文献中介绍的气井积液实验数据验证新模型的准确性，该实验通过数码摄像机捕捉微观液滴实际形状，采用数字流量计对注入高压气体计量。液滴实验先采用小气量实验，然后加大注气量，待注入液体使井底积液实现稳定不再增长，这时的注气量即为临界产量，同时观察并记录压力传感器的数据，该数据即为对应井口压力值。观察数字温度计数据，得到该组实验对应的井口温度。实验发现在低压条件下，液滴最小为1 mm，液滴合并最大为4～5 mm，运动液滴近似为椭球体的形状，高宽比约为0.9。且实际气流中液滴会由于力矩的不平衡出现翻滚从而减小有效迎流面积。采用相同的条件，计算气井携液临界流量与实验数据对比，如图8所示。从图中可知，在相同条件下计算携液临界流量，Turner公式系数为6.6，李闽公式系数为2.5。与实验数据相比，Turner公式计算的结果偏大，而李闽公式计算结果偏小。考虑液滴尺寸为4.5 mm、变形后高宽比为0.9时，新模型公式系数为4.75，与实验数据吻合最好。

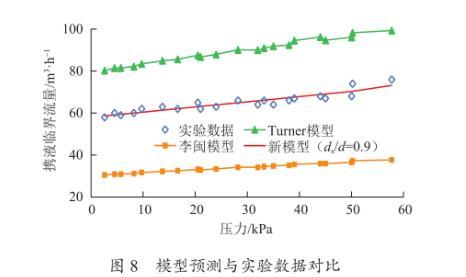
图8模型预测与实验数据对比

7、结论

（1）建立了考虑界面张力、液滴尺寸和液滴变形影响的携液临界模型。模型首先通过分段拟合界面张力实验数据，建立界面张力公式，然后引入变形液滴曳力系数公式及液滴变形程度和液滴尺寸之间的关系式，得到更加符合实际的携液临界流量模型。

（2）界面张力随压力和温度变化，压力越大、温度越高，气水界面张力越小；气体相对密度越大，气水界面张力越小。当压力和温度分别为0～40 MPa和20～200℃时，界面张力范围为30～75 mN/m，考虑界面张力影响的携液临界流量比界面张力为常数时的计算精度要高。

（3）液滴尺寸和变形对携液临界流量影响较大。当液滴特别小时，液滴在压差下基本不发生形变，液滴基本呈球形，曳力系数近似0.44；随着液滴直径越大，液滴越容易变形，液滴高宽比越小，曳力系数越大，携液临界流速变小。考虑了液滴尺寸和液滴变形影响的新模型与实验数据吻合良好。