2理论模型及计算方法

2.1理论模型

假设一不可压缩液滴在均匀加热的固体表面上不断蒸发,如图1所示,液滴初始最大厚度为,流动方向尺度为L,壁面温度为w.由于ε=≪1(图1中的H˜,L˜仅为表示清楚,不代表真实比例),因此可应用润滑理论(上标～表示有量纲量,下同).

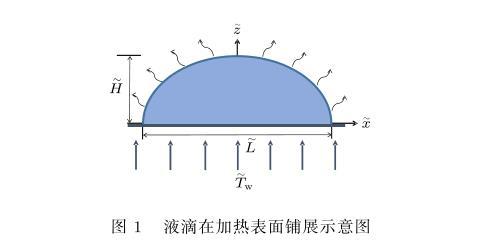
图1液滴在加热表面铺展示意图

液滴运动过程的控制方程包括连续性方程、动量方程和能量方程:

界面处的蒸发流量与界面温度有关,可表示为

为避免接触线处出现应力奇点,在水平方向施加Navier滑移边界条件:

壁面温度满足

由于固-液、固-气界面张力目前仍难以通过实验直接测量,假设固-液、固-气界面张力不随温度改变,而气-液界面张力与温度满足线性关系:

将控制方程和边界条件采用下式进行无量纲化:

通过无量纲变换和保留数量级≥Ο(ε),可得无量纲控制方程组为

无量纲边界条件为无量纲形式的界面张力与温度关系为

液滴表面温度为

采用积分法可得液滴厚度的演化方程为

(27)式右侧依次代表毛细力、重力、热毛细力和蒸发在液滴运动过程中的作用.

液滴在理想光滑表面上,在三相接触线处,Young方程为

为描述接触角迟滞影响,采用以下线性经验关联式描述前进接触角和后退接触角与迟滞角之间的关系:

式中,A≥0是与粗糙度无关,与液体性质有关的常数;迟滞角Δθ与表面粗糙度和化学异质性有关.

接触线处的液滴高度为零,即h(x=xcl=xcr,t)=0,其中xcl和xcr分别代表左侧和右侧接触线位置.采用下式描述接触线移动速率与接触角间的关系[28](下标c代表接触线):

式中,B和m为常数;θ为动态接触角;υc>0代表接触线向外铺展,υc<0代表向内收缩.

计算初始条件为

式中,F(x)=0.5[1+tanh(20x)].

基于Karapetsas等提出的坐标变换法,将瞬态物理域(x,t)映射到固定计算域(x',t'),

液滴运动区域设定为–1≤x'≤1,时间导数表示如下:

(36)式用于替换控制方程(27)的相应项.

数值求解采用Freefem++14.3,该软件是求解偏微分方程的强大工具,是一款免费的、开放源代码的有限元计算软件,目前已经比较成熟地运用在各类数值模拟中,对于液滴、液膜的流体数值计算也很常见.该软件采用Delaunay算法生成离散偏微分方程所需网格,具有网格自适应和移动网格生成的功能;采用稀疏矩阵存储格式,内存需求少,计算速度快,是求解复杂区域问题的高效计算软件.

2.2计算模型验证

参照朱仙仙等用4µL去离子水在加热温度为60°的玻璃表面上的蒸发实验数据,换算得到无量纲参数,各参数取值为:ε=0.1,A=0.39,B=0.007,m=3,C=–0.004,Bo=0.007,Ca=0.5,K=10,E=1×10-3,Ωlg=0.003.首先,为了验证数值模拟结果的准确性,将接触角和接触线随时间变化的实验结果无量纲化后与模拟值进行对比,结果如图2(a)和图2(b)所示.可以看出,Δθ=0.27时的模拟值与实验结果总体符合良好,即采用考虑接触角迟滞的理论模型可更准确地反映液滴的运动过程.值得注意的是,朱仙仙等所给实验结果并未呈现液滴铺展阶段,可能是由此阶段变化较快、不易观测记录所致;模拟结果和实验结果有偏差的原因可能是实验时基底加热时受热不均匀或者基底传热能力不一致,也有可能是基于润滑理论建立模型时,未考虑液滴蒸气扩散所致.

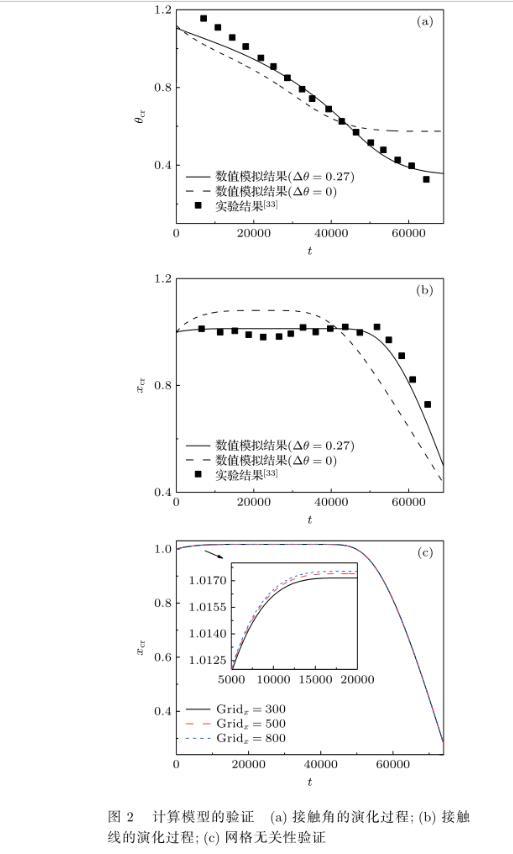
图2计算模型的验证(a)接触角的演化过程;(b)接触线的演化过程;(c)网格无关性验证

此外,模拟时进行了网格无关性验证,在x方向上对比了网格数为300,500和800的结果,发现增加网格数使计算时长增大,而各特征参数计算结果数值差距不大,以图2(c)的接触线演化过程为例,网格数为500时可同时满足精确性与高效性的要求.因此,计算中时间步长设为10–6,将[0,2]×[0,1]的计算域划分为500×2个均匀网格.因方程(27)是一维的,液滴厚度h与y方向无关,所以为节约计算时间,在y方向仅划分2层网格.