结果和讨论

在下文中，我们将介绍静态单层膜上的SFG实验，该实验显示SFG信号的异常、逐级强度变化。相比之下，BAM显微镜图像在SFG实验的长度尺度上显示出均匀的单层。在SFG实验过程中，通过减少通量或连续移动单层，可以记录单层的真实SFG响应。最后，给出了椭偏测量实验，以补充SFG结果。

静态单层上的SFG测量：SFG光谱的密度依赖性。在图1的中间面板中，在每个分子的不同区域（密度）描绘了DPPC在H2O上的SFG光谱。通过在CHCl3中添加DPPC溶液液滴来改变密度。底部光谱来自空气−水界面，并显示来自3000至3600 cm之间氢键水分子的信号−1和一个信号从自由OH在∼3700厘米−1.20令人惊讶的是，表面活性剂DPPC的添加不会导致SFG光谱的变化，只要压力保持在我们的检测限以下。尽管表面存在脂质，但在SFG实验中未检测到它们，也不会对水结构产生可检测的影响：在没有脂质的情况下以及在低密度下存在DPPC的情况下，SFG光谱无法区分（见图1的下面板）。考虑到我们的SFG实验的信噪比，可以测量到10%的强度下降。由于强度取决于数密度的平方（所有其他条件都相等），我们得出的结论是最多3−4%的游离OH基团受脂质影响。值得注意的是，表面活性剂也不会影响水的结构，特别是当人们意识到脂质分子（对于完全压缩的单层膜）占据的最小面积是∼40Å2.在100Å2的水面积上，大约有三个OH分子，21,22，因此每自由OH的面积大约为∼30Å2.如果我们假设表面活性剂在表面上的统计分布，那么可以预期，在每个分子108Å2的脂质密度下，大约三分之一的游离OH基团将受到影响，这将使游离OH处的SFG信号下降到原始强度的一半。表面活性剂也没有出现在光谱中：在2800到3000厘米之间没有可检测到的CH振动−图1中的1为低密度的中间面板-与ROKE4和陈一致。9在图1的中间板中可见，通过在氯仿中加入更多的DPPC液滴来增加表面活性剂的密度导致压力上升和SFG谱的变化：CH振动出现在频率上。∼2850（CH2对称拉伸），∼2880（CH3对称拉伸），以及∼2950厘米−1（CH3费米共振和CH3不对称拉伸），9,23水氢键信号增加，自由OH峰消失。界面系统有效地从水/空气界面逐步转变为水/表面活性剂界面。为了量化光谱变化的突然程度，我们在压缩单层膜时连续测量了压力和SFG光谱。通过添加0.5μL DPPC溶液，直到每个分子的面积为∼达到100Å2。DPPC在H2O上的结果如图2a所示。如图2a中的插图所示，通过整合SFG光谱的不同光谱窗口可获得不同的曲线。对于这些实验，红外脉冲的中心频率保持固定，以在连续压缩期间获得足够的信号强度。因此，在本实验中，我们只能同时测量表面活性剂和H键水的CH振动。随后在较高的红外频率下测量了氢键水和自由OH键的信号。从图2a可以清楚地看出，在85Å2左右仅改变表面活性剂密度的几个百分点对系统有显着影响。之前曾报道过CH信号的突然上升，4,9但水光谱的急剧变化尚未报道。水信号的增加似乎是一个循序渐进的过程：大约在每DPPC分子85到50Å2之间，SFG强度是恒定的。将脂质密度改变1.5倍对单层内和下层水分子的信号强度几乎没有影响。就像水信号一样，脂质C−H拉伸强度也或多或少地恒定到∼每个分子50Å2（图2）。C的恒定SFG信号−文献报道了DPPC在压力等温线平台上的H振动。4,9在PSS和SPS极化下，我们观察到DPPC的SFG信号在压缩后同样急剧上升。此外，两种不同的表面活性剂，棕榈酸和1-十二醇（见图2c和d），在SSP极化下测量到类似的突然急剧上升，尽管发生台阶的每个分子的面积取决于分子（每个分子分别为20和30Å2）。因此，观察到的行为似乎是表面活性剂的一般行为：观察到的是脂质、酒精和脂肪酸。

BAM测量。为了确认表面活性剂分子存在于表面，我们进行了布鲁斯特角显微镜（BAM）测量，其结果如图3所示。DPPC的表面密度已经非常低，每分子140Å2。众所周知，当DPPC密度低于约90Å2/分子时，单层显示气相和液相膨胀相共存，分别在BAM实验中产生暗斑和亮斑。亮区的数量，代表密度更高的液体膨胀相，随着密度的增加而增加。在每个分子为84Å2时，图像没有任何对比度，显示了微米尺度上的层均匀性：系统处于液体膨胀相。该层的进一步压缩（密度增加）导致小而明亮的星形畴，在液体膨胀相的暗背景上呈现液体凝聚相。等温线在这里显示了一个平台。在平台的末端，压力急剧上升，BAM图像是均匀的：整个表面处于凝聚相。我们的BAM结果与文献一致。17,24

静态单层上的SFG测量：SFG信号的通量依赖性。尽管BAM显微镜数据显示，在每分子140Å2的情况下，液体膨胀相中含有脂质的区域是可见的，但SFG的分子是不可见的。正如引言中已经提到的，在过去，CH拉伸区域的不可见性被指定为卷曲尾巴4或无序尾巴。9然而，这种解释无法解释为什么水信号不受每个分子密度约为85Å2的脂质的影响。特别是，游离OH基团应受到脂质存在的影响，无论脂质是否卷曲。根据SFG结果，系统表现为每分子85Å2以上的水/空气。在测量位置的激光焦点中，表面似乎已清洁；所有具有液相膨胀相的畴似乎都从SFG激光光斑中移除。在这种情况下，我们可以预期台阶相对于每个分子面积的位置将取决于实验中使用的激光注量。为了验证这一假设，我们使用四倍更低的红外功率重复了SFG测量。当光束尺寸保持不变时，注量减少了4倍。从图2b中可以清楚地看出，这一步实际上是向较低的密度、较高的每分子面积移动，并且变得不那么陡峭。面板b中的插图通过显示通量与SFG信号出现时每个分子的面积之间的相关性总结了通量依赖性。显然，激光强度对SFG信号的外观有影响。这一解释也与Chen等人9的观察结果一致，即来自头部的P=O信号仅在高密度下可见，因为只有在高密度下，脂质才存在于激光焦点中。

表面“清洁”的说明。可以计算出，利用所使用的激光参数（光束尺寸、脉冲能量和频率），水界面区域将被加热。详细计算见附录。这些计算表明，对于红外光谱中吸收非常强的区域，可用的最高脉冲能量，单脉冲温度升高可达10°C。鉴于我们的激光重复频率为1 kHz，重复单脉冲加热也会产生稳态加热。由此产生的稳态温度升高可能高达数十℃。

结果，出现横向和轴向温度梯度。横向温度梯度，即沿表面的温度梯度，沿表面产生应变，进而触发水流。25如图4a所示，水将从辐照点中心径向流出。为了保存质量，来自下方的淡水将补充从辐照点流出的水。通过这种方式，将产生一个多纳型圆形Marangoni型流动池，如图4b所示。Bain等人先前提出了类似的机制。26由此产生的流动池解释了为什么激光焦点中不存在脂质。如果注量太高，则驱动脂质进入激光焦点的扩散力、熵力不足以抵消脂质离开激光焦点的水的Marangoni流。激光对表面进行了非常有效的清洁，表面上不断出现大量的淡水。随着表面密度和相关表面压力的增加，出现一个点，即流动强度不足，无法抵消表面活性剂的扩散力和熵力。虽然水仍可能在脂质单层下面流动，但单层足够坚硬，因此它仍保持在原位。在相应的表面活性剂浓度下，表面活性剂信号突然出现。这种界面Marangoni流动池的出现解释了为什么压力足够低时表面看起来很原始，为什么表面活性剂信号随着压力的增加突然出现，以及为什么信号出现的压力取决于激光注量。

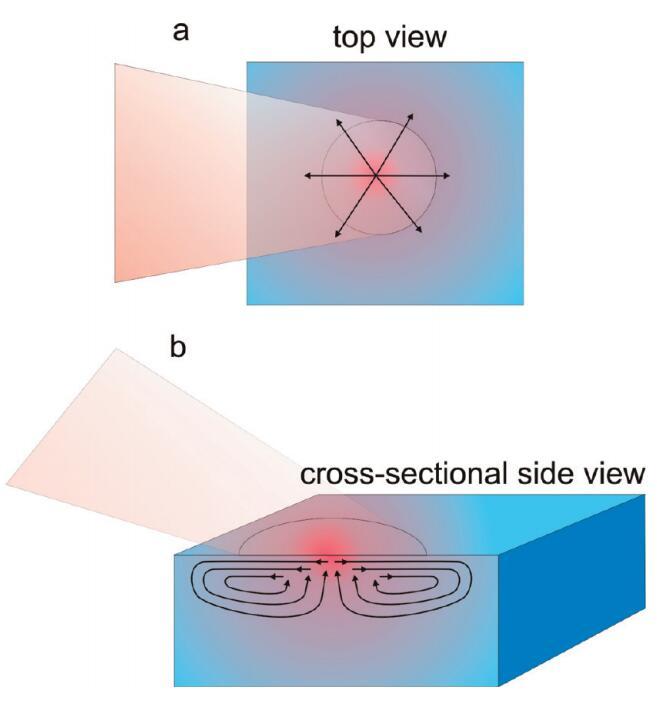
图4。水样近表面区域稳态加热引起的流动示意图。温度示意图上用颜色表示，其中红色表示热，蓝色表示冷。橙色阴影区域显示入射到表面的激光束，箭头表示温度梯度诱导流动的方向。（a）俯视图，显示近表面区域的径向位移，（b）横截面侧视图，显示产生的Marangoni流动单元。请注意，在焦点的中心，水流向上，因此表面可以有效地持续更新。

激光焦点内局部脂质密度降低的另一个原因可能是加热层时压力增加。水的表面压力将大致增加0.15 mN/m K.25。10°C的温度升高将导致裸露水面的压力增加1.5 mN/m。在顶部有脂质的情况下，这种压力增加很可能会更大，因为如果假设理想气体、温度升高10 K和密度为1018分子/m2，则仅表面活性剂层中的压力增加估计约为0.15 mN/m。显然，温度升高会导致压力升高。这种压力增加将导致单层的局部膨胀——在足够低的压力下，系统局部甚至可能进入纯气相。由于海槽的未扰动区域比扰动区域大许多数量级，因此很容易进行局部扩展。在激光点处，系统处于极低密度气相，SFG信号可能低于我们的检测限。在这种平衡热力学情况下，对于气体和液体膨胀状态的整个共存区域，预计不会出现SFG信号。系统将局部降低其压力，并且系统处于完全气态的激光光斑处。然而，我们的数据（图2b）表明，这一步骤可能已经出现在共存点，这表明平衡热力学无法解释一切。我们也可能有动力的贡献。在低红外通量下，加热不再足以使相转变为气相。

移动单层上的SFG测量：SFG光谱的密度依赖性。为了获得低表面活性剂密度下的“真实”表面SFG响应，我们在旋转槽中进行了SFG实验，如图5所示。样品以这样的方式旋转：在激光焦点处，样品以∼0.06 m/s，在这种情况下，稳态加热最小。图5a显示了水的SFG光谱−空气接口和230Å2/分子DPPC，同时旋转槽而不旋转槽。裸水界面和非旋转槽的SFG信号相同。通过旋转槽，出现CH信号，水信号增加。信号的出现是转速和红外注量之间的微妙平衡。以获得足够低的红外注量(∼1.5 mJ/cm2）我们使用相对非聚焦的红外光束（束腰∼500μm）。转速过低时，仍然看不到SFG信号；用于将脂质从病灶中排斥的激光诱导流量仍然过高。在高密度下，信号形状和强度与槽是否旋转无关（图5b）。图5c描绘了当水槽持续旋转时，DPPC在水中密度（从下到上）增加的SFG光谱。通过在氯仿中添加DPPC滴来控制脂质密度。底部光谱是空气光谱−水界面。显然，随着DPPC密度的增加，CH和H键OH信号缓慢而连续地增加，而自由OH信号也平稳地减少。

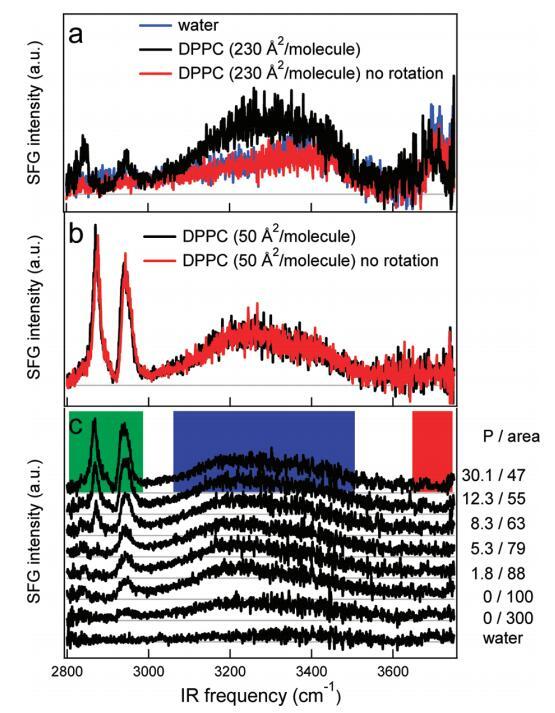
图5。（a）DPPC在水上以230Å2/分子（黑色）和不旋转（红色）槽的SSP极化的SFG光谱。样品以这样的方式旋转：在激光焦点处，样品以∼0.06 m/s。不旋转时，光谱与水相同−空中接口（蓝色）。（b）在高密度（每个分子50Å2）下，旋转（黑色）和非旋转（红色）之间没有区别。（c）裸露水面的SFG光谱（SSP极化）（底部光谱）和密度增加的水中DPPC的SFG光谱。压力（mN/m）和每个分子的面积（Å2）分别从底部到顶部增加和减少，在图表旁边给出。每个分子的面积由氯仿溶液滴的数量控制。彩色方块标记了图6中使用的积分区域。本实验中使用了相对较低的红外注量（1.5 mJ/cm2）。

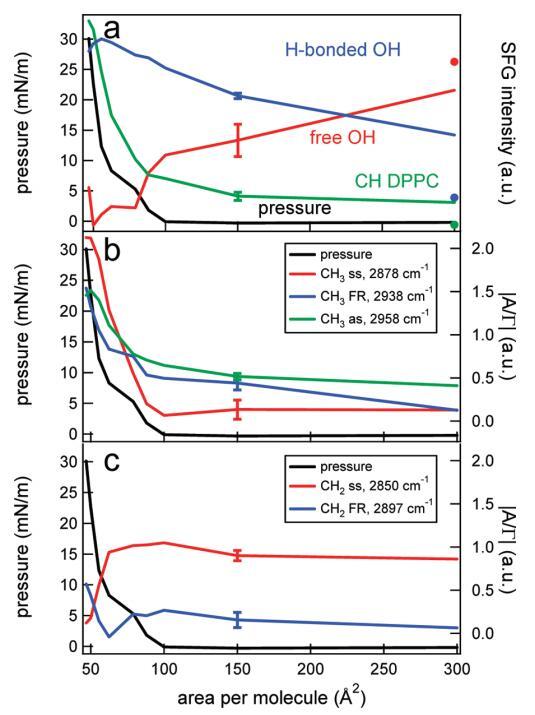
图6。（a）DPPC的CH信号（绿色）、Hbonded OH信号（蓝色）和游离OH信号（红色）的表面压力（黑色，左轴）和积分SFG强度（右轴）作为每个分子面积的函数。数据点是通过整合特定光谱区域获得的，该区域由图5的光谱中的彩色方块标记。纯水层的CH、OH和游离OH面积（在表面活性剂摊铺前测量）分别表示为绿色、蓝色和红色圆点。为清晰起见，集成SFG信号已被标准化，并且彼此略微偏移。（b）表面压力（黑色，左轴）和不同CH3共振（右轴）的绝对振幅/带宽比（|A/Γ|），通过使用洛伦兹线型模型拟合图5中的数据获得。（c）和b一样，但是对于CH2共振。典型误差条如图所示。

SFG光谱中不同振动的积分SFG强度与图6a中的表面压力一起绘制，作为每个分子面积的函数。CH强度随着表面DPPC分子数量的增加而非线性增加。水信号持续增加，而自由OH信号随着表面分子数量的增加而持续减少，正如预期的那样，当系统达到液体膨胀相时，27达到零值。原则上，在气相和液相膨胀相的共存区（如上∼每个分子100Å2），人们可能会看到波动的SFG信号，因为气相不发出信号，而液相膨胀相发出信号。用二次谐波发生器28和椭偏仪观察到了这种波动信号。29然而，此处未观察到这些波动，因为呈现的SFG光谱平均超过10分钟，这在磁畴扩散的时间尺度上很长，发生在数十秒的时间尺度上。28,29

高密度下不同的SFG光谱是激光注量的函数。通过比较在不同通量下测得的高压（高脂密度）下脂层的两个SFG光谱（图7），在CH峰处观察到差异，而水带大致相同。在相对较高的通量下（底部面板）∼10 mJ/cm2，CH2峰值为2850 cm−1仍然清晰可见，而该峰值在低通量的顶部面板中不存在(∼1.5 mJ/cm2）。此外，在高通量谱中，CH3峰的强度（2880和2950 cm−1）与低通量测量相比，相对于水而言，低通量测量。这两个观察结果清楚地表明，在高通量条件下，单层膜受到激光的影响：由于热，尾部更加无序，导致更多的凹凸不平的缺陷，因此存在CH2峰和CH3信号减弱。显然，激光的重复激发导致了从具有有序尾的凝胶状态到具有较少有序尾的液晶状态的相变。30，因为实验是在室温下进行的(∼23°C），相变温度为41°C，30我们可以得出结论，在高通量情况下，样品的稳态加热至少为18°C，考虑到基于焦点尺寸和红外光穿透深度（见附录）估计的单发温升在2到19°C之间（取决于红外频率），这并非不合理。对于低通量情况（顶部面板），稳态温升不超过18°C，因为我们仍然可以看到有序的尾部，通过停止槽的旋转指示凝胶状态。

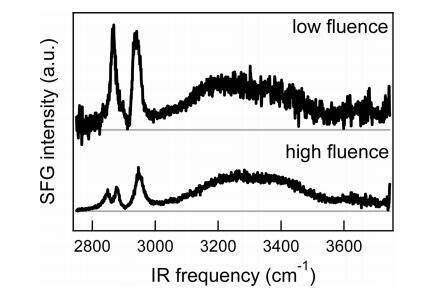
图7。高密度水上DPPC的SFG光谱（SSP极化）(∼每分子45Å2）在低浓度下(∼1.5 mJ/cm2）和高通量(∼10 mJ/cm2），单脉冲加热量分别在0.3至3°C（取决于红外频率）和2至19°C之间。为了清晰起见，对光谱进行了偏移，并根据相对红外强度进行了缩放。注意，由于在高通量下发生的热效应，形状非常不同。这两种光谱都是用非旋转槽测量的。

此外，激光的热效应在图1中每分子78Å2的面积处的光谱中已经可见，其中，引人注目的是，O−H，但不在C中−H拉伸区。这可以通过扫描C−H和O−H拉伸区域：在低频时，红外强度高于高频时，导致在C中的界面处积聚更多的热量−H区比O区小−H区域（见附录）。请注意，与穿透深度相比，激光发射之间的热扩散发生在较大的长度范围内，因此只有激光强度（而不是穿透深度）与稳态温度升高相关（参见附录图9）。一旦红外光源达到低频（C−H区域），由于更大的热梯度，由于流动，脂质被更有效地运走。如果红外频率稍高，则累积热量稍少，并且可以检测到磁畴。这解释了水信号的存在，但没有CH信号。与Casson等人26在纳秒红外激光实验中的观察结果一致，我们的数据表明，通过使用高强度飞秒红外激光，必须注意由于样品加热导致的结果失真。在这两种情况下，稳态加热主要负责观察到的畸变，因此只有激光注量是重要的。

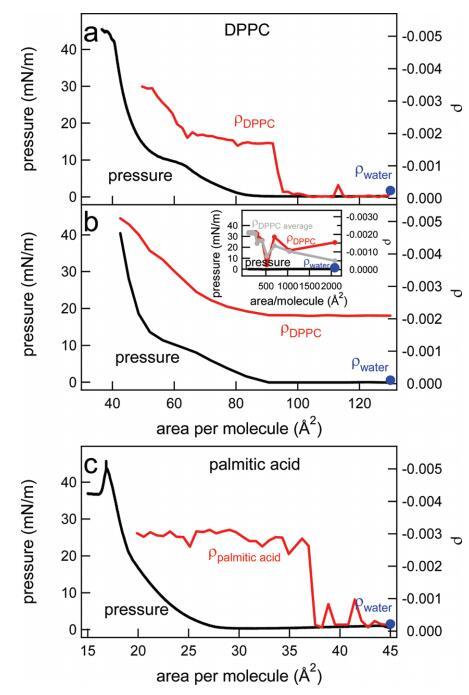
图8。（a）在制备单分子层后，通过快速添加DPPC溶液持续压缩单分子层，直到达到130Å2的每分子面积，水上DPPC的表面压力（黑色，左轴）和椭圆系数（红色，右轴）。（b）水上DPPC的表面压力（黑色，左轴）和椭圆系数（红色，右轴）是每个分子面积的函数。通过逐滴添加更多DPPC，每次滴加间隔几分钟，改变了该区域。以这种方式达到的每个分子的最小面积为2000Å2。插图显示了椭圆度系数（对于一个特定实验（红色）和三个实验的平均值（灰色））以及非常低密度下的压力。（c）在制备单分子层后，通过快速添加棕榈酸溶液，直到达到每分子45Å2的面积，连续压缩单分子层期间，水上棕榈酸的表面压力（黑色，左轴）和椭圆系数（红色，右轴）。在喷洒表面活性剂之前测量的纯水椭圆度在每个面板中以蓝色圆点表示。

椭偏仪。有趣的是，在椭偏仪中，当脂质和脂肪酸在低密度（接近零压力）下压缩层时，已反复观察到椭圆系数的一个步骤。14−18此处也观察到同样的情况：在图8a中，描述了作为DPPC每个分子面积函数的椭圆系数以及同时测量的表面压力。每个分子130Å2的反射率与水的反射率相当−空中接口。在最初通过添加氯仿溶液滴到每个分子的面积为130Å2压缩单层后，观察到与SFG数据中类似的步骤，但该步骤出现在每个分子的不同面积，95 vs 85Å2。对于棕榈酸，通过椭偏仪在∼每个分子37Å2（图8c），与SFG实验相反，SFG实验中每个分子20Å2（图2c）。与SFG实验相反，椭偏仪实验中使用的激光与分子跃迁不共振，且激光的注量非常低，因此，可以排除由于加热效应而出现的Marangoni流细胞作为信号阶跃的原因。使用IR附录中给出的相同表达式计算的温升在1s内低于0.001°C。值得注意的是，如果椭偏仪实验以不同的方式进行，不是在连续压缩下，而是通过添加更多DPPC溶液来改变面积，椭偏系数的表现非常不同（图8b）：椭偏系数中不存在不连续性。我们注意到，与这些椭偏测量结果相比，SFG结果与单层的制备方式无关。对于已经处于非常低密度的椭偏仪，即使在添加第一滴DPPC溶液后，椭圆度系数也明显不同于纯水的椭圆度系数。每个分子高达300Å2左右，该值波动，因为大小与激光光斑大小相当的液体膨胀畴在周围浮动。我们可以预期，在对多个实验取平均值后，该系数将随着密度的增加而线性增加，在这种情况下，我们可以看到一个实验的波动。事实上，从图8b插图中的灰线可以看出，平均三次实验接近这种线性关系。在较高密度下，从∼每个分子300到90Å2，当系统仍然处于气相和液相膨胀相共存时，椭圆度系数是平的。在较低密度下，其上升方式与压缩下观察到的相似（图8a）。这两种实验的主要区别在于允许系统放松和平衡的时间。在第一个实验中，在连续压缩下，快速添加DPPC溶液，直到每个分子的面积达到130Å2。在第二个实验中，该层在每个分子2000Å2时为几分钟，然后在每个分子1000Å2时为几分钟，依此类推。Ducharme等人14之前曾观察到压缩实验中低密度平台的开始取决于初始表面密度。他们认为，在低初始密度下，分子有空间定向，从而形成一个在椭偏测量中活跃的层；i、例如，分子在与表面法线类似的角度下排列和定向。14如果初始浓度过高，由于缺乏空间，分子在运动中受到限制，并陷入亚稳状态，没有或只有很少的界面双折射，椭偏仪对此非常敏感。在高初始密度下，表面活性剂层内的分子间相互作用明显阻止脂质分子的有序排列。每个分子的临界面积预计约为300Å2，即平放DPPC分子的面积。对于这种在椭偏仪中不提供任何对比度的初始动力学冷冻单层，需要显着的分子间相互作用（随着单层被压缩而变得更重要）来诱导脂质分子的集体排列。我们的观察结果与Ducharme等人的假设完全一致：对于缓慢制备的层，平台的起始密度为每分子250Å2左右的低密度（每分子的高面积），而对于初始表面覆盖率为每分子130Å2的层，台阶出现的密度要高得多。有趣的是，椭偏系数在每分子约300Å2的范围内保持不变，直到压力开始以每分子约90Å2的速度上升。尽管气相和液相膨胀相共存时的密度变化了3倍，但系数是完全平坦的。然而，BAM结果表明，压缩层会产生更多的液相膨胀相（畴变大）。只有当有效折射率或层厚度减小时，这些结果才能相互一致。使用洛伦兹线型模型（参见，例如，参考文献4）对旋转槽（图5）获得的SFG结果进行拟合表明，在椭偏系数恒定的相同密度区域，CH2对称拉伸振动的振幅也是平坦的。拟合结果如图6b和6c所示。尽管脂质密度增加，但粗齿缺陷的平均数量保持不变，表明该层改变了方向。显然，该层以这样一种方式做到了这一点，即椭圆偏振系数和CH2对称拉伸振动的SFG信号保持不变。

尽管椭偏仪和SFG在压力开始上升的表面活性剂密度之前或周围显示出信号的不连续性，但起源似乎不同。在SFG测量中，该步骤与水相的加热有关。由于这种加热，表面活性剂将净流出激光焦点，如图4所示。在低表面活性剂密度下，表面在激光焦点处被清洁：所有脂质分子有效地从SFG激光光斑中去除。我们想强调的是，共振红外激光的极低通量（每脉冲的温升小于3°C，且红外处于OH波段的最大值）已经足以将表面活性剂的畴移出焦点，如图2和图5所示。在较高的表面活性剂密度下，排斥激光力不再来自驱动分子进入激光焦点的扩散力。发生这种情况的密度，以及SFG信号出现的位置，以与等温线类似的方式取决于表面活性剂的类型。压缩时，压力越早偏离零，在压缩等温线中观察到从无SFG信号到信号的步骤越早。我们想强调的是，只有通过使用旋转槽刷新激光脉冲之间的样品，才能完全消除SFG实验中观察到的台阶。只有在这种情况下，稳态加热才足够低，以避免磁畴排斥出激光焦点。通过旋转槽，可以在非常低的密度下测量“真实”SFG光谱。

在椭偏仪中，由于峰值功率低得多，且辐射与分子跃迁不共振，因此激光不会对该层造成相同程度的干扰。椭偏仪中的步骤起源于亚稳状态，该状态发生在初始脂质密度过高时。对于这样一个系统，它需要大量的压缩来诱导分子从不可见的无序态转变为具有集体排列尾的可见态。然而，发生该步骤的密度取决于该层的制备。如果该层是通过让分子有足够的空间和时间松弛而制备的，则该步骤甚至完全不存在。从未对齐尾到对齐尾的过渡（负责椭偏测量中的步骤）不能解释SFG情况下观察到的行为，因为如果表面活性剂的尾对齐，则氢键和游离OH的水信号不应显示一个步骤。

结论

我们已经阐明了在表面活性剂单分子膜的SFG实验中观察到的信号随表面活性剂密度的函数突然增加的原因。我们通过测量水信号证明，表面活性剂被激光脉冲从探测区域置换。旋转槽的使用避免了样品的稳态加热导致光清洗，并使样品在空间上均匀。这允许在整个密度范围内测量DPPC水上CH和OH区域的“真实”SFG光谱。液态膨胀相光谱中CH2振动的存在表明分子的尾部不是有序的。在液体凝聚相中，仅存在来自CH3基团的振动：脂质有序，没有粗糙缺陷。水信号持续增加，直到达到液体冷凝相。自由OH峰（代表顶部没有DPPC的水分子）减少，直到不再存在气相。如果使用非旋转槽，则在密度非常高的情况下不会检测到SFG信号，因为液体膨胀相畴很容易被同一激光器从激光光斑中移除。布鲁斯特角显微镜显示了这些区域，结合红外激光束，可能能够可视化稳态加热的效果。

附录

单次激发的温升可以根据给定频率下的光束尺寸和吸收截面来计算。根据参考文献31，朗伯吸收系数为α（λ）=4πk（λ）/λ，其中λ为光的波长，k为折射率的虚部。用于频率为3100 cm的红外激光束−1，α为0.36μm−1.忽略表面约1%的光反射，并考虑到从原始透射强度I0到入射点距离l处的剩余强度I为I/I0=e−α*l，可以容易地计算出界面区域的平均吸收功率，其中50%的红外光被激光脉冲吸收。

具体而言，在实验部分给出了高通量情况下（图1、2（图2b除外）和7底板）的红外光束（功率：6μJ；束腰：200μm；入射角：40°）和水的热容（4.2 J/gK）的详细信息，在表面激光束尺寸和50%穿透深度形成的体积上，我们获得了平均9 K的单次激发温度增加。在吸水率的峰值（在∼3300厘米−1与∼4μJ IR），在50%穿透深度为0.6μm时，上升甚至达到19 K，而在CH区域（在∼2940厘米−1与∼6μJ IR）上升为2 K，50%穿透深度为10μm。对于低通量情况（图5、图6和图7，顶部面板），束腰大约大2.5倍，导致通量大约低6倍。因此，单次激发的温度跳变也降低了6倍。

对可见光光束的相同计算表明，可见光光束与加热过程无关：可见光光束的单次升温仅为0.06 mK，因此可以忽略不计。

然而，本文中描述的效应不是由单次激发引起的，而是由稳态加热引起的。假设水的热扩散系数为1.11×10−3 cm2/s，假设垂直于水面的一维热扩散，可以计算出在1 ms（两次激光发射之间的时间）内，热扩散距离界面约20μm。更准确地说，在脉冲撞击表面1毫秒后，热量呈高斯分布，在最大值处有一半宽度∼20μm。由于我们所有频率下的红外穿透深度都小于扩散长度20μm，因此1ms时的热分布或多或少与频率无关。因此，1 ms时表面的热量主要由红外功率决定，该功率在低频时较高（即，在C−H区域）在低频下产生更多稳态热。在CH和OH振动激发后的两个不同时间，从此类计算中获得的热分布如图9所示。

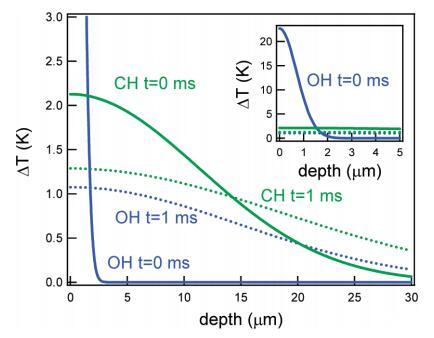
图9。对于与CH（绿色）或OH（蓝色）振动共振的红外光束，温度随着进入水层的深度而升高。实线和虚线分别表示t=0和t=1 ms。插图显示了相同的图形，但带有扩展的yaxis。

作者信息

笔记

作者声明没有相互竞争的经济利益。

致谢

这项工作是“材料研究基金会（FOM）”研究项目的一部分，该项目由“荷兰材料研究基金会（NWO）”资助。作者感谢Remco Fokkink和Marc Jan van Zadel对椭偏仪实验的帮助，并非常感谢Ron Shen、Colin Bain和Harald Pleiner的许多有益讨论。