容易想象，一般地，浮在水面上的物体距离较近时会有明显的相互靠近的趋势。例如，在有水的盆子里放入一些泡沫塑料颗粒或小木块(小木屑也行)，它们会有明显的聚集在一起的趋势，且会聚集到盆子边缘。但进一步实验就会发现一些奇怪的现象。

若水盆的水足够多，以至于水的液面高过了盆子边缘，盆里的泡沫塑料就不会贴着盆子了，而且反而盆子边缘会对泡沫塑料产生一种排斥作用。

于是猜测吸引或排斥与液面形状有关。一般地，水会在浮在水面的物体的接触面上“爬”一点，就是浸润，于是再做实验:使物体和水不浸润。由于手头没有蜡，我用硬塑料卡片来模拟非浸润。卡片密度比水大，躺放水面上的时候，是水的张力托住了卡片。于是水与卡片接触的位置比水面低，这就模拟了一个非浸润的情形;而容器壁的非浸润也很好模拟，如上段所述，只要把水装到比容器口高就行。

如此观察浸润与非浸润物体之间(容器壁也可看作物体)的吸引与排斥情况，得出结论:

浸润与浸润间:相互吸引

浸润与非浸润间:相互排斥

非浸润与非浸润间:相互吸引

为何会出现这样的现象？能否严格地用数学证明并推导出相关等效力的公式？

解答：

终于抽点时间完成这一问题，关于所谓的数学推导我会附上参考文献。在这儿只是做科普定性分析。先说结果，楼主的结论是完全正确的，其原因是亲疏水物体在水面上引起表面张力的对称性变化。

我们由水面上两个球形的物体做理想分析，现在先看亲水的球形的物体在水面上使水面升高的情形。如图1所示，亲水物体由于其毛细作用，附近水面上升，不过水面升高后以指数函数在两侧下降，其影响距离大致为毛细作用力的距离，即2.7 mm。大于2.7 mm时，重力与表面张力相比重力占据主导地位，液面几乎不再上升。

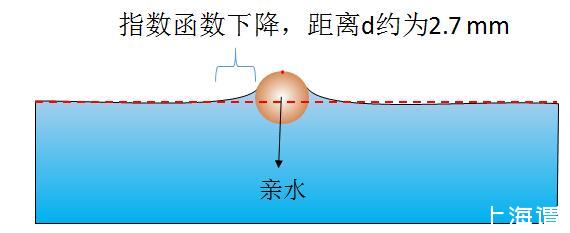
图1亲水物体使周围水面升高，影响范围约为2.7mm，此时液体表面张力垂直向下

下面开始考虑两个亲水物体。如图2所示，两个亲水的物体距离很远时，各自引起水面上升，由于每个只能影响2.7 mm的区域，所以互不影响。

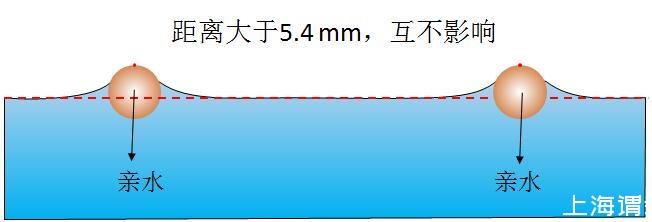
图2当亲水球体距离很大时，每个表面张力的合理都向下，互不影响

这时，让两个亲水的物体缓慢靠近，当一个处于另外一个的毛细作用力范围时，由于毛细作用的相互耦合作用，两个球形颗粒之间的液面会比两侧要高，这就打破了原来每个球形颗粒所受液体表面张力的对称性，使表面张力的合力不再是垂直向下。出现了水平方向的分力，表现为相互吸引，如图3。

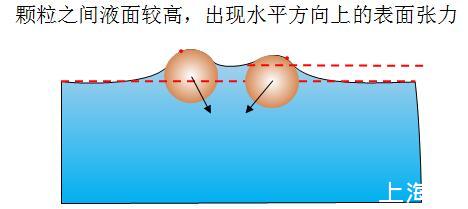
图3两个亲水物体相互靠近时，互相毛细作用下，中间液面比两侧较高，表现为相互吸引

同样的分析也适用于疏水颗粒之间，如图4所示，疏水的颗粒使周围的液体液面下降，作用范围同样为2.7 mm，液面从颗粒向两侧以指数函数上升。

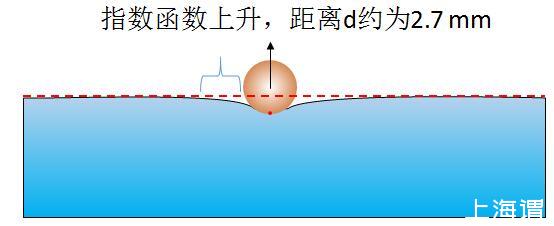
图4单个疏水颗粒的表面张力合力向上

当两个疏水颗粒距离较远时，毛细作用力互不影响，不再画出。但是一旦相互靠近，同样的作用下，毛细作用力的耦合作用使颗粒之间的液面要比两侧都低，这同样打破了原来单个颗粒两侧表面张力的对称性，出现了水平方向上的合力，其效果使之相互吸引，如图5所示

图5两个疏水颗粒在水平表面张力分力下相互吸引

那么一个亲水颗粒和一个疏水颗粒呢？

当其距离很远时，互不影响，如图6所示。

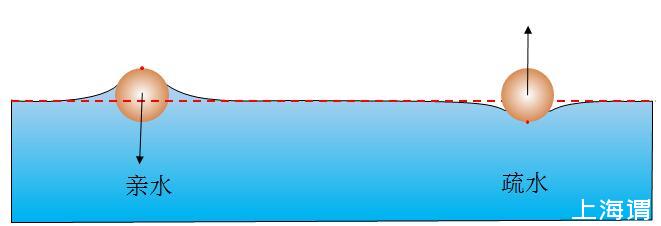
图6亲疏水颗粒距离较远，各自所受表面张力时对称的，没有水平分力

当其相互靠近时，亲水的颗粒的毛细作用力使疏水的颗粒附近液面升高。疏水的颗粒使亲水的颗粒附近的液面下降，其效果如图7所示。这同样打破了原来表面张力的对称性，然而这时出现的表面张力为互相排斥。

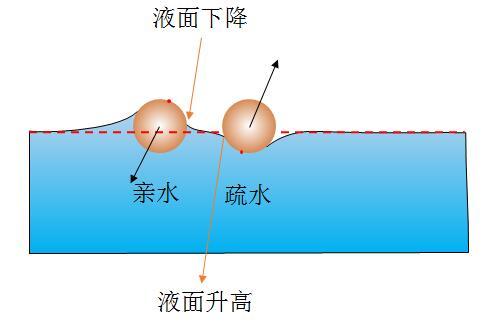
图7亲水疏水颗粒相互使液面变化，打破原来所受表面张力的对称性，出现相互排斥的表面张力

其规律是：亲水的物体使液面升高，亲水的物体之间靠近有加强作用，使中间的液面比两侧要高。同理，疏水的使中间液面更低。而这两者都表现为相互吸引。

亲水的使疏水的固体附近液面没那么低，疏水的使亲水的物体附近液面没那么高，表面为相互排斥。

定量分析参考文献为：

Peter A.Kralchevsky,Nikolai D.Denkov.“Capillary forces and structuring in layers of colloid particles”Current Opinion in Colloid&Interface Science 6(2001).383-401.

2.R.Di Leonardo,1 F.Saglimbeni,2 and G.Ruocco.“Very-Long-Range Nature of Capillary Interactions in Liquid Films”Phys.Rev.Lett.100,106103(2008)