2理论模型

2.1液态Ag表面张力与温度的关系

研究[20]表明，液态金属的表面能与内聚能之间存在比例关系，表达式为：

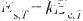(1)

式中，Es,T和Ec,T分别表示温度为T时的单位面积表面能(J/m2)和摩尔内聚能(J/mol)；k为比例系数，其与表面相和本体相的原子配位数有关。

由于表面能和表面张力通常具有相同的大小和维度，在没有严格区分的情况下，认为二者是等价的。根据式(1)可以得到液态Ag的表面张力与内聚能之间的关系式，即：

(2)

式中，γAg,T表示温度为T时液态Ag的表面张力(N/m)，Tm表示Ag的熔点(K)，γAg,Tm和Ec,Tm分别表示熔点温度下的表面张力和摩尔内聚能。其中，摩尔内聚能与温度和定压热容有关，表达式为：

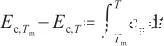(3)

式中，cp表示定压热容[J/(mol·K)]。

当温度升高到临界温度时，液态Ag完全转变为气态。此时，表面张力降低为0。根据式(2)和(3)，可以得到：

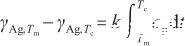(4)

式中，Tc表示液态Ag的临界温度(K)，γAg,Tc表示临界温度下的表面张力，并且γAg,Tc=0。由此得到比例系数k的表达式，即：

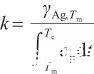(5)

联立式(2),(3)和(5)，可以得到：

(6)

此外，表面张力是原子间作用力的宏观表现，可表示为单位长度的力，取决于各个原子之间的作用力及单位长度上的原子数目。然而，式(6)仅反映了各个原子之间的作用力，并没有涉及单位长度上的原子数目。考虑液态Ag热膨胀对表面张力的影响，引入线膨胀系数α来描述液态Ag在膨胀过程中单位长度上原子数目的变化。因此，可以将式(6)变换为如下形式：

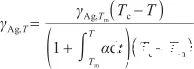(7)

式中，α表示线膨胀系数(K-1)。

式(7)表示在整个温度范围内，液态Ag的表面张力与温度的关系，相关参数的取值列于表1[21-26]。

表1模型计算中使用的物理参数[21-26]

Table 1 The physical parameters used in the model calculations[21-26]

通过对式(7)关于温度T求导，可以得到液态Ag表面张力的温度系数，其表达式为：

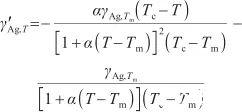(8)

式中，γ΄Ag,T表示液态Ag表面张力的温度系数[N/(m·K)]。

从热力学角度看，表面张力系数的负值表示为表面过剩熵SAg(T)，即：

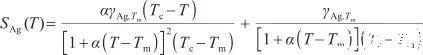(9)

2.2液态Ag-O系的表面张力研究

对于液态Ag-O系，可以将其划分为三个相，包括：气相(g)，指O2分子；本体相(b)，表示液态Ag内部区域；表面相(s)，位于气相(g)和本体相(b)的交界处，具有一定的厚度。上述三个相的分布示意图如图1所示。

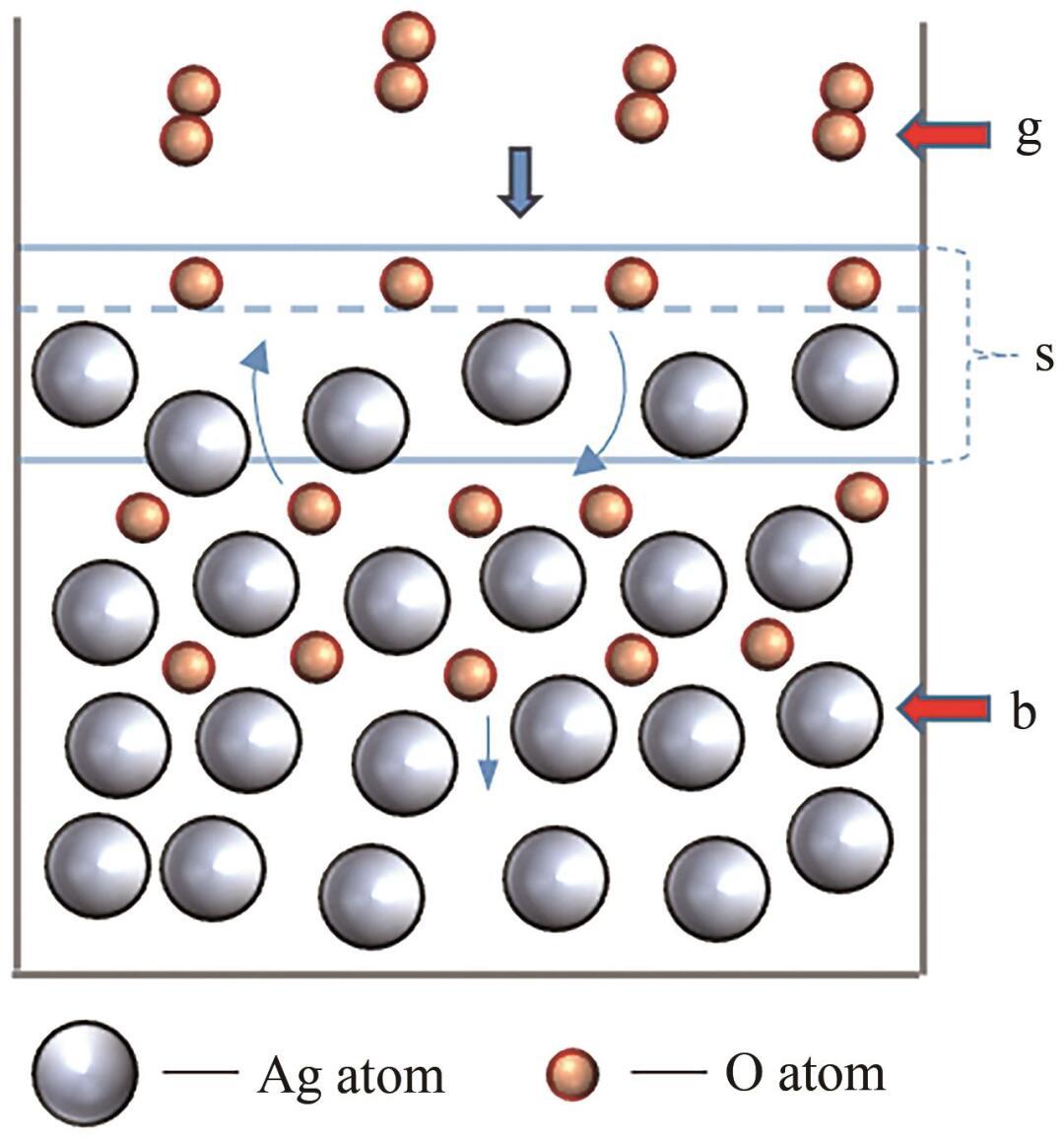
图1 Ag-O系的相分布

根据图1，首先O2分子从气相(g)扩散至表面相(s)；其次在Ag的催化下解离为O原子，并发生化学吸附；最后，O原子从表面相(s)扩散至本体相(b)。整个过程可以表示为：

(10)

与此同时，本体相(b)中的O原子倾向富集于表面，以降低自由能。假设表面相(s)中的空位(V)数量有限，并且每个空位只能被一个O原子占据，则O原子的表面偏析过程可以表示为：

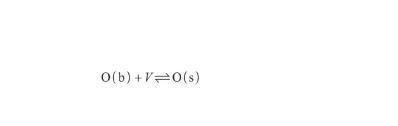(11)

根据式(10)和(11)，当系统的表面相(s)和本体相(b)之间达到热力学平衡时，可以使用Butler方程[17]来描述表面张力，即：

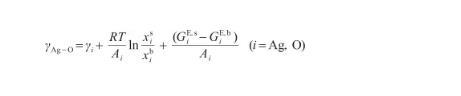(12)

式中，γAg-O表示Ag-O系的表面张力(N/m)，γi表示纯组分i的表面张力(N/m)，R为气体常数[J/(mol·K)]，x和x分别表示组分i在表面相和本体相中的摩尔分数(mol/mol)，Ai为组分i的摩尔表面积(m2/mol)，G和G分别表示表面相和本体相中组分i的偏摩尔过剩自由能(J/mol)，并且G=λG，其中λ为表面相和本体相的原子配位数之比[27]。G可由摩尔过剩自由能GE,b表示，其关系式为：

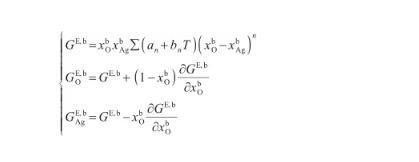(13)

式中，GE,b表示Ag-O系的摩尔过剩自由能(J/mol)，n,an和bn均为待定参数，可以通过相图计算获得。

另外，液态Ag的摩尔表面积AAg可以通过以下表达式[28]计算得到：

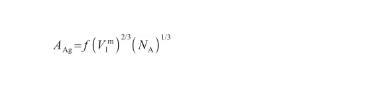(14)

式中，V表示液态Ag的摩尔体积(m3/mol)，NA为阿伏伽德罗常数(6.02×1023)，f表示几何因子(无量纲)。其中，V和f的计算式为：

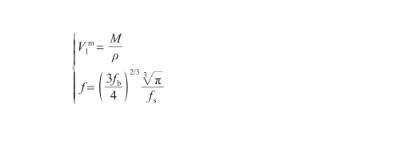(15)

式中，ρ为液态Ag的密度(kg/m3)，M为Ag原子的摩尔质量(kg/mol)，fb和fs分别为本体相和表面相的原子堆积比率。表面相原子总是紧密排列，以达到自由能最小的状态，通常认为其原子堆积比率与Ag(111)晶面相同[28]，即fs=0.906；对于本体相，随着温度升高，体积逐渐增大而原子堆积比率相应降低。因此，fb的计算式为：

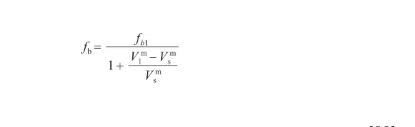(16)

式中，fb1表示为本体相在熔点温度下的原子堆积比率，且fb1=0.704[28]；V表示固态Ag在熔点温度下的摩尔体积(m3/mol)。

2.3 Butler方程的简化

由式(12)和(13)可以看出，Butler方程计算较为复杂。考虑液态氧的表面张力很小[14]，可以认为γO≈0。另外，由于Ag-O系中O原子数远小于Ag原子数[29]，可以将Ag-O溶体视为理想溶体。此时，GE,b=G=G=0。根据文献[18]，当式(12)所示的Butler方程用于描述理想溶液时，通过假设系统内两组分具有相等的摩尔表面积，可以得到改进的Butler方程。这个改进的Bulter方程能够推导出Gibbs吸附方程和Langmuir方程，被认为是表面张力和溶液吸附的根本方程。因此，令AAg=AO，将式(12)变换为：

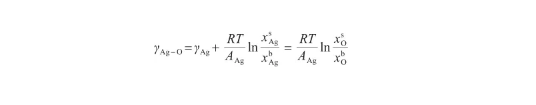(17)

为了验证这种近似处理的合理性，使用理想溶体近似模型计算Ag-O系的液相线，并将结果与实验相图进行比较。

对于Ag-O系，两组元的原子百分数之和为1，即：

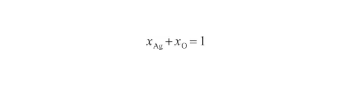(18)

式中，xAg和xO分别为系统中Ag原子和O原子浓度(at%)。

液相线表示系统由液态转变为固态的初始温度或其逆过程的终了温度。通过液态、固态中的Ag原子浓度来描述这一可逆过程，从而有：

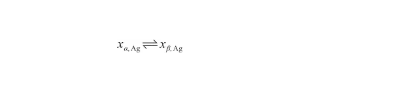(19)

式中，xβ,Ag和xα,Ag分别表示Ag-O系液态、固态中的Ag原子浓度(at%)。

Ag-O系固-液转变过程进行到一定限度时，系统达到平衡，自由能不再发生变化，且为最小。同时，固态、液态中的Ag原子浓度也不再发生变化，平衡系数KI表示为：

(20)

根据Van't Hoff方程，平衡系数KI与反应焓变之间有如下关系：

(21)

式中，Hm为Ag的摩尔熔化热(J/mol)。

将式(20)代入式(21)中，并对温度从T到Tm积分，得：

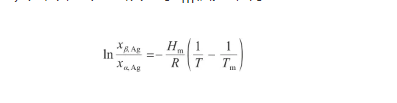(22)

式中，Tm为Ag的熔点(K)。

由于固态Ag的溶氧量接近于0，可以认为xα,Ag≈1。联立式(18)和(22)，得：

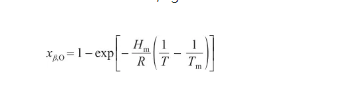(23)

式中，xβ,O为液态Ag-O系中的O原子浓度(at%)。

根据式(23)计算了Ag-O系的液相线，结果如图2所示。从图中可以观察到，理想溶体近似模型的计算值与实验相图[29]非常吻合。因此，可以将Ag-O系视为理想溶体。

图2 Ag-O系液相线

联立式(17)和(18)，将Ag原子浓度代以O原子浓度，从而有：

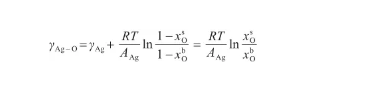(24)

根据式(24)，可以将表面相的O原子浓度x表示为：

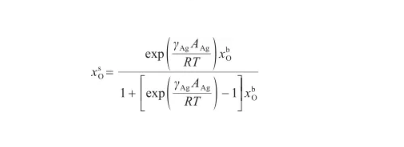(25)

由于式(25)与改进的Langmuir方程[30]具有相同的形式，因此将其变换为：

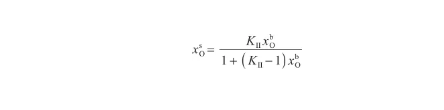(26)

其中，KII表示表面偏析平衡系数[18]，表达式为：

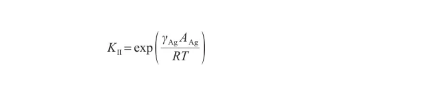(27)

将式(26)代入式(24)，可以得到液态Ag-O系的表面张力关于温度和O原子浓度的表达式，即：

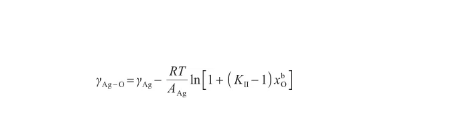(28)

根据Sieverts定律[31]，Ag-O系的饱和O氧原子浓度与氧气压力的平方根成正比，即：

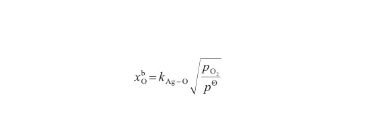(29)

式中，kAg-O为Ag-O系的Sieverts系数，是温度的函数；pO2表示气相的氧气压力(kPa)，pΘ表示标准大气压(101 kPa)。

显然，式(10)中的平衡系数与式(29)中的Sieverts系数相等。因此，可以得到Sieverts系数与标准吉布斯自由能变之间的关系式，即：

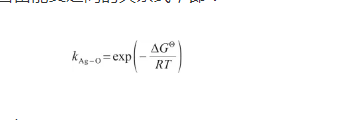(30)

式中，ΔGΘ表示液态Ag溶氧过程的标准吉布斯自由能变(J/mol)，其计算式[29]为：将式(30)代入式(29)中，得：

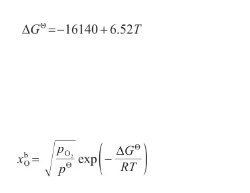(31)(32)

结合式(28)和(32)，可以得到液态Ag-O系的表面张力关于温度和氧气压力的表达式，即：

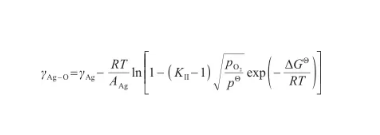(33)

2.4液态Ag-O系表面的氧吸附行为

根据Gibbs吸附方程，表面过剩量的定义式为：

(34)

式中，Γ2,1表示二元系中组分2相对于组分1的表面过剩量(mol/m2)，μ2为组分2的化学势(J/mol)。

通过对式(28)关于x求偏导，可以得到：

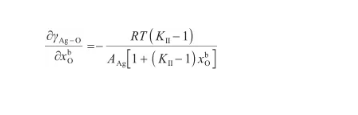(35)

在液态Ag-O系中，O原子的化学势(μO)表示为：

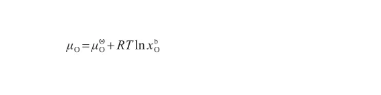(36)

其中，μ表示O原子的标准化学势(J/mol)。对式(36)关于x求偏导，得：联立式(35)和(37)，得：

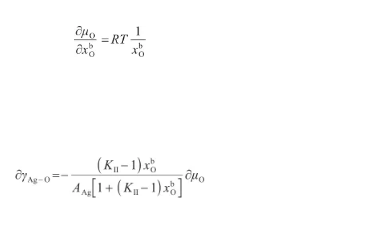(37)(38)

结合式(34)和(38)，可以得到O原子的表面过剩量，表达式为：

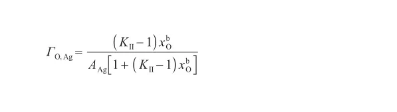(39)

将式(32)代入式(39)中，可以得到表面过剩量关于温度和氧气压力的表达式，即：

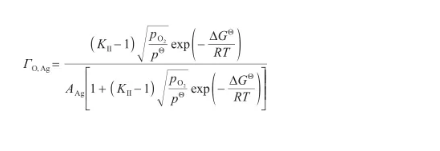(40)

此外，在式(26)左右两边同时除以x，得到表面偏析因子(η)的表达式。结合式(32)，将其变换为：

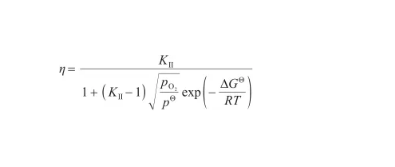(41)

液态Ag-O系表面张力和表面过剩量计算、氧气压力和温度的预测模型——摘要 、简介

液态Ag-O系表面张力和表面过剩量计算、氧气压力和温度的预测模型——模型

液态Ag-O系表面张力和表面过剩量计算、氧气压力和温度的预测模型——结果与讨论