借助MATLAB工程计算平台，通过程序设计完成了“正丁醇水溶液表面张力的测定”应用软件的开发。在完成录入压差实验数据后，不仅可以自动计算和填入溶液的表面张力，还能够实现溶液表面张力与浓度定量关系的希斯科夫斯基经验方程(Szyszkowski′s equation)中待估参数的求解，并用以求导供给吉布斯公式计算溶液的吸附量，进而推算溶液饱和吸附量和正丁醇分子的截面积。软件的操作过程简便、直观、高效，避免了人工数据处理、绘图的烦琐和人为误差，可提高实验结果的准确性和重现性。

1、表面张力测定原理

表面张力是流体的重要物性数据，与诸多工业领域应用联系密切，如化工传质分离、食品药品加工、矿物浮选、制冷工程等，但表面张力无法直接通过热力学微分关系式从状态方程导出，精确可靠的表面张力数据只能通过实验精密测量得到，常用方法包括毛细管上升法、最大气泡压力法、挂环法、滴体积法等静力学法和震荡射流法、毛细管波法等动力学法[1]。

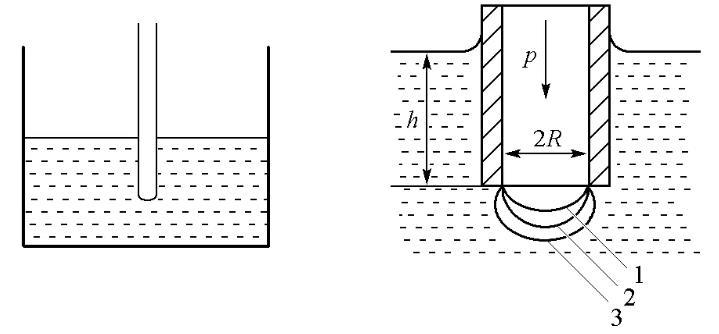
图1表面张力的泡压法测定原理图

由于最大气泡压力法的器材易得，且易于学生理解表面张力的原理，因而一直是教学中测定液体表面张力的一种常用方法[2]。如图1所示，测定时将一根毛细管插入待测液体内部，从管中缓慢地通入惰性气体对其内的液体施以压力，使管端形成气泡逸出。当所用的毛细管管径较小时，可以假定所产生的气泡是球面的一部分；但是在气泡生成及发展过程中，气泡的曲率半径会随惰性气体的压力变化而改变。当气泡的形状恰为半球形时，气泡的曲率半径最小(即毛细管半径R)，此时根据Laplace方程，管内外压差达最大，其值Δpmax=p-ρgh可由差压计测量得到[3]。利用最大压差和毛细管半径即可计算表面张力σ：

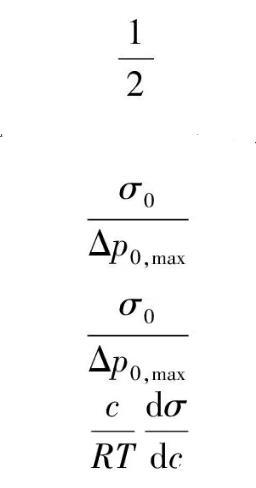
若采用同一支毛细管和差压计，在相同温度下测定已知表面张力的液体(如25℃蒸馏水，σ0=71.97mN·m-1)在毛细管中的最大压差Δp0,max，则有：

针对实验采集与计算获得有限多个不同浓度c下的表面张力σ，传统的数据处理方法是手工绘制这些离散点的趋势曲线，并求出曲线上指定几个点的切线斜率，进而求算表面吸附量。然而，手工图解作切线这一步的误差较大，结果重复性差，难以得到准确的结果。对此，本文介绍在物理化学实验“正丁醇水溶液表面张力的测定”中，借助MATLAB工程计算平台[5]，选择希斯科夫斯基关联方程(Szyszkowski′s equation)，经由少数测量数据点关联与求解正丁醇溶液表面张力和浓度之间的定量关系数学模型，并借此求算曲线上任意指定浓度下的切线斜率，进而求算该浓度下的表面吸附量，以提高数据处理的效率和质量。

2、实验部分

2.1仪器及试剂

仪器：AF-02型数字式微压测量仪，数控恒温槽，5mL和10mL移液管各一支，碱式滴定管1支，50mL容量瓶9个，样品管1个，毛细管1个，抽气瓶1个，锥形瓶1个，玻璃漏斗1个。

试剂：正丁醇(A.R.)及其不同浓度的标准溶液。

2.2实验步骤

①用体积法准确配置浓度为0.025、0.050、0.075、0.10、0.15、0.20、0.25mol/L的正丁醇水溶液各50mL。

②如图2示，调节恒温槽的温度在25℃，打开AF-02型数字式微压式测量仪的电源，预热20min。

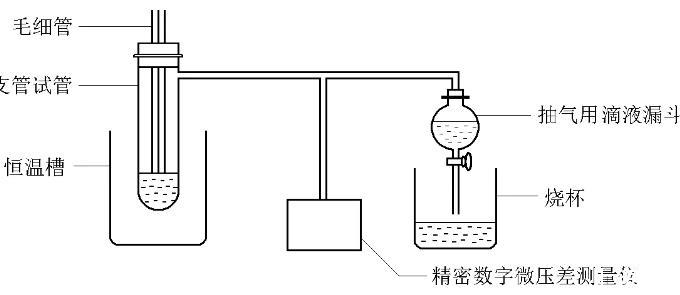
图2表面张力测定的实验装置

③先用洗液洗净大试管与毛细管，再用自来水和蒸馏水洗净；在大试管中注入适量蒸馏水，使毛细管端口刚好与液面垂直相切；将大试管安装在恒温水溶液内，用小漏斗给抽气瓶装满自来水。

④连接好装置，使其无漏气。在体系通大气的条件下按校零按钮，使显示器值为0.000kPa。

⑤测定蒸馏水的Δp0,max。打开抽气瓶的活塞，使瓶内水缓慢滴出，导致大试管逐步减压，待气泡形成速度稳定(约5～10秒出一个气泡)后，读出气泡脱出瞬间的Δp0,max；连续读3次，取平均值。

⑥按照上述方法测定不同浓度正丁醇溶液的Δpmax值。不同溶液测定时须按低浓度到高浓度的次序测定；测定每一样品时只需要用同样浓度的溶液淌洗3次即可，并对测量数据进行记录(例见表1)。

⑦实验完毕，清洗玻璃仪器，整理实验台。

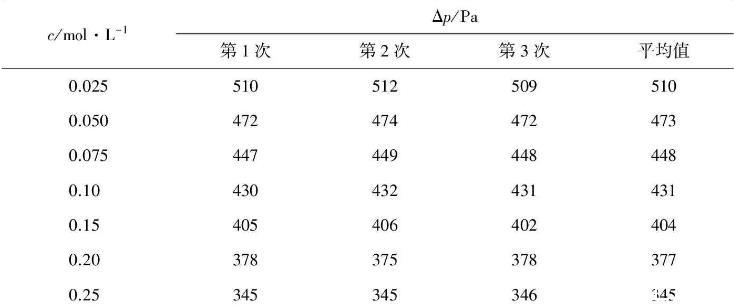
表1不同浓度正丁醇水溶液的表面张力测定数据

3、实验数据处理及MATLAB实现

3.1表面张力的希斯科夫斯基经验方程

考虑到正丁醇系短链醇、醛、酮、酸、胺等第二类表面活性物质，在低浓度下其表面张力随浓度增大在起始时降得较快、随后呈减慢的特点，适宜选用希斯科夫斯基经验方程来拟合溶液表面张力σ与溶液浓度c之间的非线性关系[6]。

式中σ0为溶剂蒸馏水的表面张力，α和β为物系待估计的模型参数。

3.2饱和吸附量和溶质分子截面积的计算

在一定温度下，吸附量Γ与溶液浓度c的关系可由Langmuir单分子层等温吸附式表示[7]。

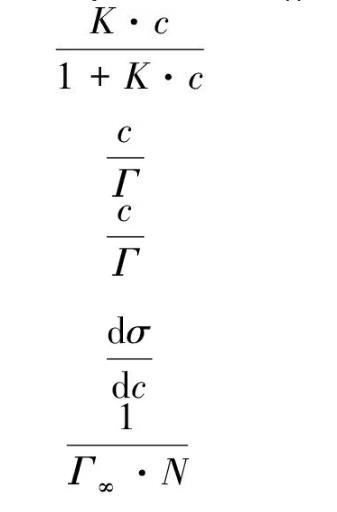
式中N为阿伏加德罗常数。

3.3用MATLAB实现表面张力及表面吸附量的计算

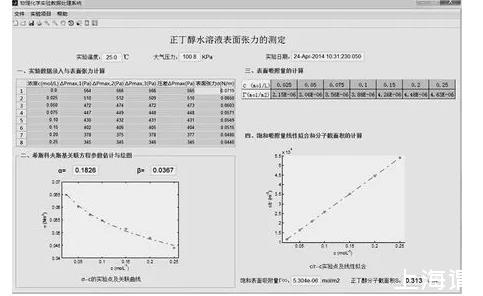
图3所示的“正丁醇水溶液表面张力的测定”实验数据处理软件由4个单元模块构成：①实验数据录入和溶液表面张力的程序自动计算；②表面张力与浓度关联的希斯科夫斯基经验方程的参数估计与图形绘制；③基于吉布斯公式完成溶液表面吸附量的计算；④饱和吸附量的线性回归求解及正丁醇分子截面积的计算。

在第一步的数据录入表格过程中，当完成第一行c=0.0的蒸馏水3次压差平行测定数据后，软件将自动完成其平均压差的计算和自动填充，然后在录入物性手册中查得25℃蒸馏水的表面张力为0.07197N·m-1，毛细管常数λ将由程序算出，并作为程序内存变量用于数据表格中不同浓度溶液的表面张力σ的计算。

4、结论

正丁醇是表面活性物质，其表面吸附量随溶液浓度增大升高，并最终趋于饱和吸附。在本实验的数据处理上，选用希斯科夫斯基经验方程进行关联与拟合，通过Gibbs吸附等温式计算溶液吸附量，通过线性回归计算饱和吸附量，计算结果符合理论情况，可以较好地反映正丁醇溶液的特性。另外，在数据处理的最后步骤中，正丁醇分子截面积的计算结果也与文献值吻合较好，能满足实验精度要求。

基于MATLAB工程计算平台开发设计的“正丁醇水溶液表面张力的测定”应用软件可用于进行实验数据计算和绘图，可以快速、客观地得到实验结果，避免了手动作图的主观性和人为误差。