合作客户/
拜耳公司 |
同济大学 |
联合大学 |
美国保洁 |
美国强生 |
瑞士罗氏 |
相关新闻Info
-
> 海洋环境表面活性物质来源及对海洋飞沫气溶胶数浓度、粒径分布、理化性质的影响(二)
> 纯水表面张力与液膜拉伸形变量关系|纯水表面张力测试数据
> 基于微纳米气泡的井口注气装置可改变油水界面张力,提高原油的采收率
> 矿浆表面张力对黄铁矿与磁黄铁矿浮选回收率的影响(三)
> 不同浓度6∶2氟调磺酸的表面张力测定仪器及结果(一)
> 新型POSS基杂化泡沫稳定剂表面张力测定及对泡沫压缩性能的影响(二)
> 3种反应型阳离子Gemini表面活性剂合成、表征和性能测试(下)
> 农药残留超标检测,会用到表面张力仪吗
> 表面张力仪应用:研究活性磁化水对无烟煤尘的湿润作用(二)
> 仲醇聚氧乙烯醚硫酸盐平衡和动态表面张力及应用性能研究(二)
推荐新闻Info
-
> 两类农用防雾涂层表面张力的深度计算与比较分析(二)
> 两类农用防雾涂层表面张力的深度计算与比较分析(一)
> 药液表面张力、喷雾方法对雾滴在水稻植株上沉积的影响(三)
> 药液表面张力、喷雾方法对雾滴在水稻植株上沉积的影响(二)
> 药液表面张力、喷雾方法对雾滴在水稻植株上沉积的影响(一)
> 烷基二苯醚/烷基苯混合磺酸盐静态表面张力、金属腐蚀性及净洗力测定(二)
> 烷基二苯醚/烷基苯混合磺酸盐静态表面张力、金属腐蚀性及净洗力测定(一)
> 全自动张力测定仪揭示子细胞表面张力对胞质分裂结局的主导作用(二)
> 全自动张力测定仪揭示子细胞表面张力对胞质分裂结局的主导作用(一)
> 烟道气与正己烷对稠油表面张力的影响机制研究(三)
热力学模型计算MgO-B2O3-SiO2-CaOAl2O3富硼渣表面张力(二)
来源:中国有色金属学报 浏览 1109 次 发布时间:2024-08-13
2 MgO-B2O3-SiO2-CaO-Al2O3体系熔渣表面张力模型的建立
Butler假设熔体表面相内组分与体相内组分在热力学上都达到平衡,推导出表面张力与热力学性质之间的关系(Butler方程)。本模型基于Butler方程计算熔渣表面张力,熔渣表面相和体相内组分通过熔渣结构离子与分子共存理论来确立。本模型主要假设如下:1)熔渣表面相与体相都遵守熔渣结构离子与分子共存理论,即组元结构都由简单离子、分子和复合分子组成,熔渣表面相和体相中简单离子和分子进行着形成复合分子的动力学质量平衡反应,且表面相和体相中形成复合分子的反应都遵守质量作用定律;2)熔渣表面相和体相中各组元的质量作用浓度和熔渣表面张力符合Butler方程:
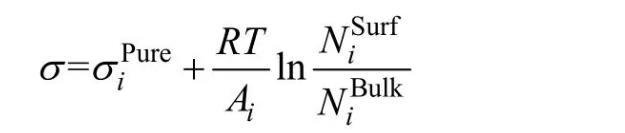
式中:σipure表示纯组元和Al2O3)的表面张力;Ai为纯组元i的摩尔表面积,其中L为校正因子,熔渣中设为1.091;N0为阿伏加德罗常数,Vi为组元i的摩尔体积);R和T分别表示摩尔气体常数和绝对温度;为组元i在表面相或体相的质量作用浓度。
根据共存理论以及上述确定的MgO-B2O3-SiO2-CaO-Al2O3富硼渣体系熔渣中存在的结构单元,定义熔渣中成分分别为。结构组元作用浓度符号表示为:
所有组元总平衡摩尔数表示为∑ni。各组元作用浓度表达式为:
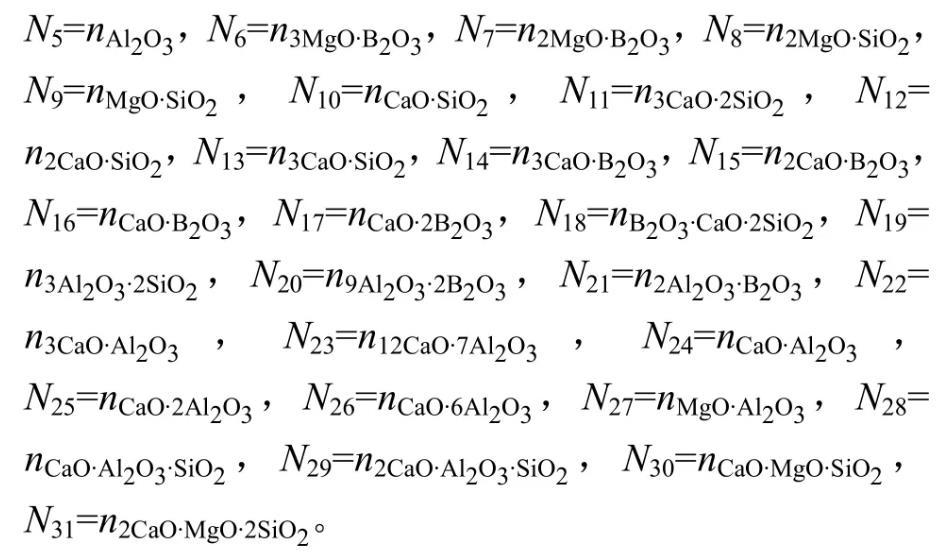
在1773~1873 K温度范围内,熔渣中各组分之间形成复杂分子的反应式及其达到平衡时的标准Gibbs自由能(以纯物质为标准态)和质量作用浓度的表达式如表1所列,其中所有反应的平衡常数可通过的关系式进行计算。
MgO-B2O3-SiO2-CaO-Al2O3渣系中质量平衡公式如下:
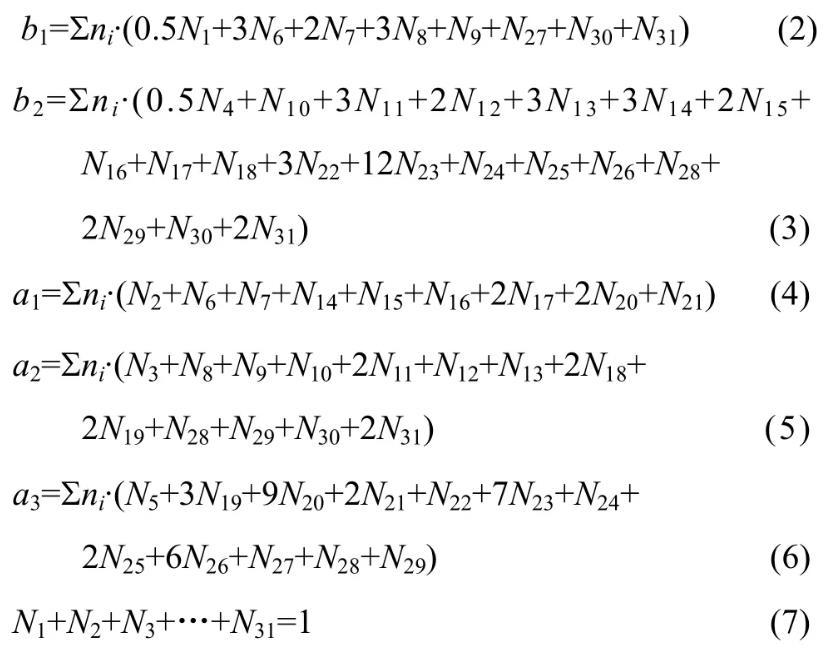
因此,由表1和式(2)~(7)建立计算MgO-B2O3-SiO2-CaO-Al2O3渣系中结构组元和离子对作用浓度Ni的控制方程,其中N6~N31由N1~N5表示出来。在一定温度下,熔渣成分代入该方程组,采用迭代法计算出所有结构组元和离子对的作用浓度。
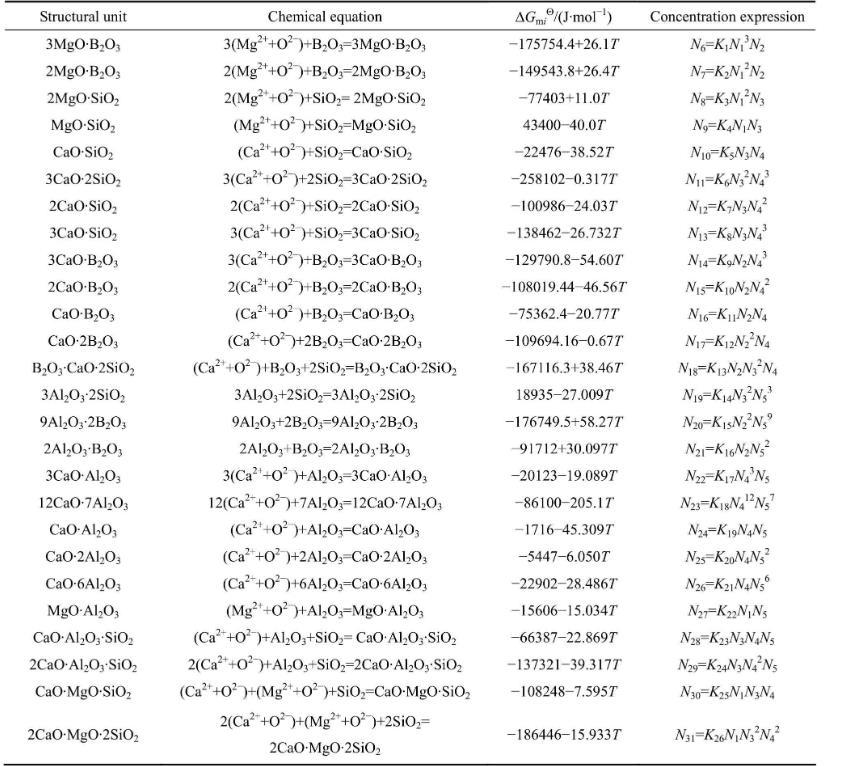
表1 MgO-B2O3-SiO2-CaO-Al2O3渣系中复杂分子的化学反应及标准Gibbs自由能和作用浓度的表达式
对于MgO-B2O3-SiO2-CaO-Al2O3体系,依据Bulter方程,其表面张力可以分别表示为
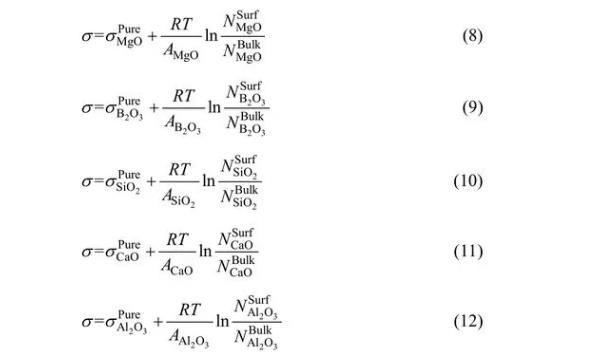
依据上述描述,建立模型可计算熔渣表面张力,其中,NiBulk可以通过熔渣成分的摩尔分数和基于熔渣结构离子与分子共存理论的形成复合分子的化学平衡计算得出。然后进一步基于共存理论和Butler方程,通过已知量NiSurf、σiPure和Ai,利用方程(8)~(12)可计算出σ和NiSurf值。MgO-B2O3-SiO2-CaO-Al2O3渣系中σiPure和Ai数据可见表2和3。
3计算结果及讨论
3.1表面张力的计算值与实测值对比
为了验证本模型计算结果的准确性,需将计算结果与文献实验数据进行对比。富硼渣相关体系中,已有B2O3-CaO体系、B2O3-SiO2-CaO体系、B2O3-CaOAl2O3体系、B2O3-SiO2-CaO-Al2O3体系和MgOB2O3-SiO2-CaO-Al2O3体系的表面张力实验数据的报道,相关体系的组分范围及温度范围如表4所列。本研究中计算了上述体系的表面张力计算值,并与文献实验数据进行了对比,对比结果如图1和表4所示。5个体系文献实验结果与计算结果总平均相当误差为9.03%。大多数熔渣的表面张力实验误差一般为±5%~10%,由此可知,本模型计算的熔渣表面张力值与实验值吻合较好。比较结果显示,B2O3-SiO2-CaO体系和B2O3-CaO-Al2O3体系偏差较大,这一方面可能与表面张力高温测量难度和精度导致的误差有关,另一方面本模型未考虑熔渣中部分组元会存在饱和现象。由于氧化物纯物质的熔点偏高,计算温度下采用的氧化物纯组分表面张力数据由已有纯物质的实验数据进行合理的外推得到,这些也可能对模型计算结果带来一定的误差。
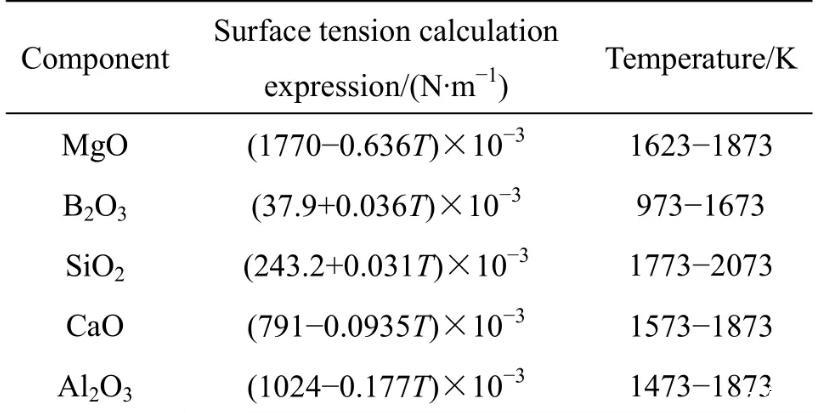
表2纯组元表面张力与温度的关系

表3纯组元摩尔体积与温度的关系
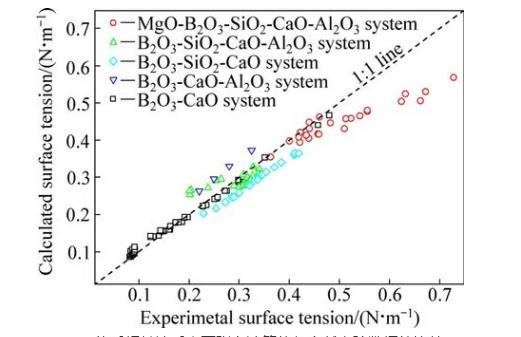
图1 MgO-B2O3-SiO2-CaO-Al2O3体系相关渣系表面张力计算值与文献实验数据的比较
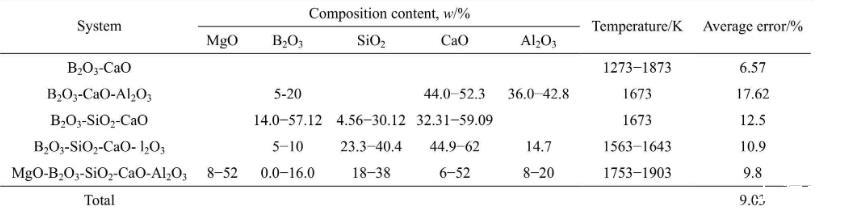
表4富硼渣相关实验渣系组分、温度及相对平均误差
热力学模型计算MgO-B2O3-SiO2-CaOAl2O3富硼渣表面张力(一)










