2多频超声波信号与界面张力之间的相关性分析

2.1多频超声波信号的幅频响应分析

实验共选取175组不同界面张力的变压器油进行实验。图4为超声波接收器接收到的三相信号的幅频响应图，所选取的5组变压器油样的界面张力值分别为27.8、32.3、36.1、41.1、55.9mN/m.

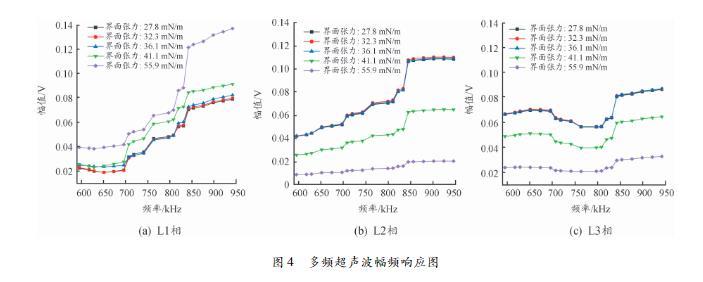
图4多频超声波幅频响应图

图4（a）为超声波接收器T1接收到的信号L1的幅频响应，可以观察到在同一检测频率下，界面张力值越大的变压器油样对应的超声波幅值越大，即变压器油样的界面张力值与L1相信号幅值存在正相关关系。所选取的5组油样的L1相信号幅值变化趋势大致相同，即随着超声波检测频率的增加，L1相的幅值逐渐增大，且L1相幅值的增幅较为明显的检测频率段为中频段700——850kHz,低频段590——700kHz和高频段850——1000kHz的幅值增幅较为平稳（不同界面张力值的变压器油样的L1相超声波信号幅值差较大的频率段为高频段）。L1相信号为超声波信号在待测介003质变压器油界面反射传播被接收到的信号，可以作为分析变压器油界面张力时的基准信号。图4（b）所示的L2相超声波信号的幅值随检测频率的变化趋势与L1相一致，但变压器油样的界面张力值与L2相信号幅值存在负相关关系。图4（c）所示的L3相超声波信号的幅值变化趋势和幅值、界面张力之间的关系都与L1相有所不同。通过观察可以得到，L3相超声波信号的幅值响应曲线呈现出比较明显的“凹”字形，即在中频段呈现“凹槽”状，低频段和高频段较为平缓，且在整个检测频率范围内，不同界面张力的变压器油样对应的L3相超声波信号幅值差值变化不明显。

2.2多频超声波信号的相频响应分析

图5为超声波接收器T1和T2接收的5组不同界面张力的变压器油样的L1、L2和L3三相超声波信号的相频响应图。从图5（a）中可以观察到，由超声波接收器T1接收的信号L1的相位变化趋势大致相同，且均在707.9、843.4kHz和696.6、832.1kHz处相位分别出现2次的谷值和峰值。如图5（b）所示，与基准信号L1相信号相比，虽然不同界面张力的油样对应的L2信号的相位图皆分别存在2个谷值和峰值，但各相位所对应的频率点分布由于界面张力的不同而各有不同。由图5（c）可以观察到L3相信号的相位变化趋势，在检测频率范围内，不同界面张力的油样在相位频谱上出现峰值和谷值的次数也不尽相同。

这是由于2个超声波接收器所接收到的三相超声波信号传播所经过的路径和周期不同，导致对应的相角不同。L2和L3的相频响应图变化趋势无相对明显的变化规律，但超声波信号在传播过程中由于发生超声弛豫、吸收、散射等现象导致相角的不同，其信息包含在相位频谱中，对于分析变压器油界面张力具有重要作用。

综合以上对幅频响应和相频响应所做的分析可知，在不同检测频率下，超声波信号的幅值和相位信息都能够体现超声波信号在待测介质变压器油中传播时的声衰减情况，即通过分析超声波信号在变压器油中传播的幅值、相位等信息可分析变压器油的品质信息。

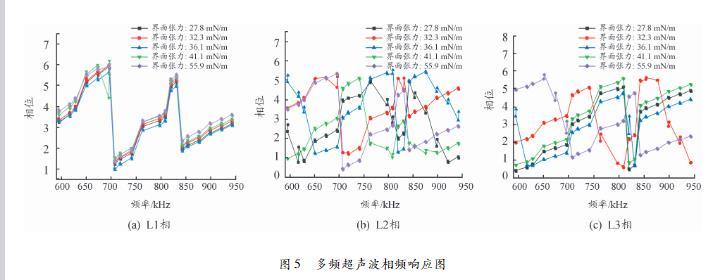
图5多频超声波相频响应图

3基于神经网络的变压器油界面张力预测模型的建立

3.1多频超声波数据的降维预处理

多频超声平台检测175组油样后得到的超声波信号数据为包含超声波信号的幅值、相位、声速和飞行时间在内的242维数据，为避免在回归预测时由于高维度数据造成的“维度灾难”等问题，在建立变压器油的界面张力预测模型前，采取KPCA对采集到的242维数据进行降维处理。

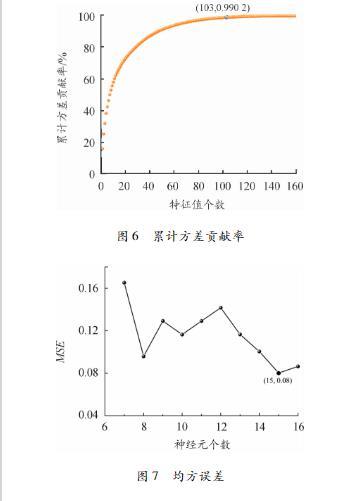
不同特征值个数对应的累计方差贡献率如图6所示，在能够保留原始多维数据的最大信息的基础上，得到累计方差贡献率为99%的103维数据，作103姚远，等：基于KPCASSAENN的变压器油界面张力预测为回归预测模型的输入。

3.2人工神经网络和参数优化算法

3.2.1ENN

通过分析采集到的多频超声数据可知变压器油样的界面张力值同超声波信号幅值、相位等存在非线性关系。ElmanJL提出的动态递归神经网络——ENN,包括输入层、隐含层、承接层和输出层。承接层可作短期存储，作为延时算子，进行内部反馈和存储历史数据，使得ENN具有记忆功能。ENN中连接权重的随机设置对于回归预测的结果造成误差，使神经网络在训练的过程中难以达到全局最优。图7展示了神经网络的均方误差随隐含层神经元数量增加的变化情况，可得当神经元数量为15时，ENN的均方误差最小，为0.08,所以隐含层和承接层的神经元的数量为15.

3.2.2SSASSA是模拟麻雀群体觅食和反捕食行为提出的群智能优化算法。图8展示了SSA优化ENN连接权重的流程。

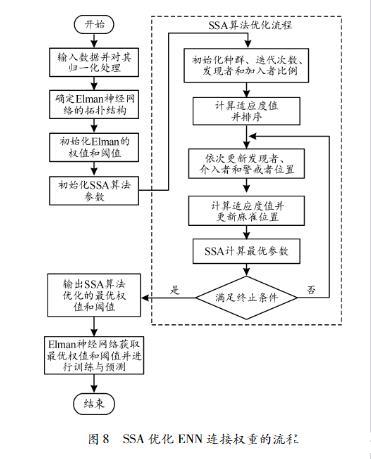
图8SSA优化ENN连接权重的流程

其步骤如下：

1）对实验的175组油样数据集进行训练集和测试集的划分。对175组变压器油样的超声波数据集进行划分，随机划分为140组的训练集和35组的测试集。

2）确定输入数据和输出数据并对数据进行归一化处理。其中，将经过KPCA降维得到的103维数据作为ENN预测模型和SSAENN预测模型的输入，输出为145组变压器油样的界面张力值。

归一化方法用于消除幅值、相位、声速等不同指标数据之间的量纲影响，将其量化在[0,1]的区间内。归一化方法的公式为：

x′=a+x-xmin

xmax-xmin

×（b-a）（6）

式中：x′代表在[0,1]区间内量化后的数据，x、xmin、xmax分别代表样本的原始数据及原始数据的最小值和最大值，a和b分别代表归一化后的最大值和最小值；

3）确定ENN的拓扑结构并对神经网络的权值和阈值进行初始化；

4）根据ENN的神经网络结构，计算出需要优化的变量元素个数；

5）SSA参数的初始化。具体参数分别为初始麻雀数，麻雀初始位置，发现者和加入者的占比情况，迭代次数上限值，上、下边界值，种群警戒值和安全值等参数；

6）SSA优化ENN的权值和阈值，适应度函数设置为ENN预测的均方误差，循环SSA优化过程，不断更新麻雀群中发现者、加入者和警戒者的位置等参数直至最大迭代次数，终止SSA;

7）将SSA优化后得到的最优权值和阈值参数输出传递至ENN,以最优的SSAENN模型训练和预测数据。

3.3预测模型的预测效果分析

图9给出了以140组样本为训练集对ENN和SSAENN预测模型进行训练后，其余未参加训练的35组样本的界面张力预测值。与测试集的界面张力实测值相比，ENN预测模型的预测值整体差值较大，预测差值最大为14.58mN/m,最小为1.38mN/m;SSAENN预测模型的整体预测差值较小，个别变压器油测试样本的预测差值较大，预测差值最大为6.08mN/m.

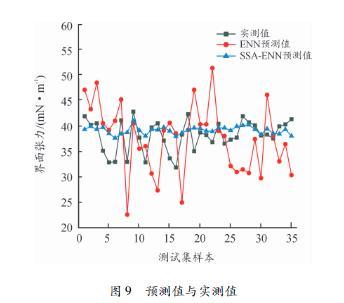
图9预测值与实测值

图10为35组变压器油测试集样本相对预测误差折线图，观察可得ENN预测模型的相对预测误差起伏较大，最高达到39.52%,平均相对预测误差为16.67%,而经过SSA优化后的SSAENN模型预测误差起伏相对较小，大多分布在相对预测误差为0的分界线的附近，平均相对预测误差为6.53%.对比SSA优化ENN前后对界面张力的预测效果，ENN预测模型的准确率为83.33%,SSAENN神经网络预测模型的准确率达到了9347%,达到了通过多频超声检测对变压器油界面张力的有效预测效果。

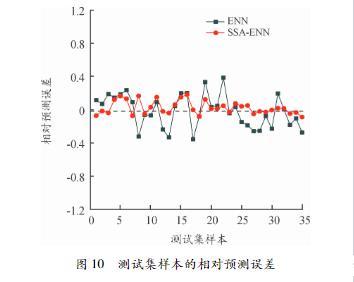
图10测试集样本的相对预测误差

通过观察SSAENN预测模型测试集各样本的相对预测误差，有5组样本的预测误差相对较大，超过15%,分别为17.35%、17.50%、15.91%、1602%和19.06%.为分析SSAENN预测模型中误差异常高的5组样本，对油样进行其他油务常规实验指标的检测，分别为微水含量、击穿电压、介质损耗因数。表2为GB/T7595—2017对运行中变压器油的质量要求。表3为预测误差较大的油样参数。由表2和表3可知，虽然5组变压器油样的界面张力和介质损耗因数满足国标要求，但微水含量和击穿电压均不满足国标要求，其中5组油样的微水含量分别超标9.42、16.11、1283、10.94、42.83mg/L,击穿电压离达标分别还差17.4、27.5、21.2、13.3、18.6kV,说明预测相

对误差较大的5组变压器油样都发生了劣化，导致预测误差相对较大。

表2GB/T7595—2017规定的运行中变压器

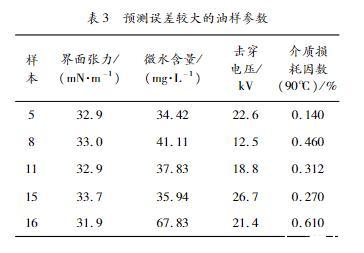
表3预测误差较大的油样参数

4结论

基于多频超声波检测技术和人工神经网络对变压器油的界面张力进行了分析和研究，对实验中选取的175组变压器油样进行界面张力的测定和多频超声波检测，通过对比5组不同界面张力的幅频响应和相频响应，分析了超声波信号同界面张力之间的关系，对实验采集到的242维数据运用KPCA降维至103维后，结合人工神经网络建立了基于ENN和SSAENN的2种界面张力预测模型。对比SSA优化前后预测模型的准确率，结果显示SSA优化后的SSAENN神经网络预测模型的准确率达到93.47%,预测效果优于ENN神经网络预测模型。与界面张力传统检测方法相比，多频超声波检测方法检测时间短，且检测重复性好，因此基于多频超声波检测技术和KPCASSAENN神经网络建立的预测模型对界面张力的识别具有可行性，为电力行业变压器油的品质检测提供了新的思路。