2结果与分析

2.1铺展因子和铺展速度

2.1.1铺展因子

若一个具有初始球形当量直径D0以及初始面积S0的液滴在撞击过程中经过铺展时间t后的铺展直径为D，铺展面积为S，且此时铺展线速度为U，则定义相应的无量纲铺展因子D*、无量纲铺展速度U*、无量纲铺展面积S*和无量纲铺展时间t*分别为

若固体表面静止，则切向韦伯数为零。

具有一定初始动能的液滴在撞击表面后向外铺展，与此同时液滴的黏性力和表面张力阻碍铺展。液滴到达最大铺展之后开始回缩，此时表面张力则是回缩的驱动力，而黏性力是回缩的阻力。

如图4(a)所示，黏度较大的液滴受到的黏性力较大，其铺展直径和最大铺展直径均较小，不发生回缩现象。如图4(b)所示，具有较小表面张力的乙醇液滴在铺展过程中受到的阻力较小，其达到最大铺展直径的时间较长，最大铺展直径较大。然而，由于较小的表面张力难以克服黏性力，导致无法产生回缩。

图4不同物性和操作条件下铺展因子的变化

如图4(c)所示，具有较大初始动能的液滴克服黏性力和表面张力之后的剩余能量更多，铺展直径和铺展时间均得以增加。当固体表面处于运动状态时，液滴的铺展直径为液滴沿固体表面运动方向的铺展长度。图4(d)的结果表明，随着固体表面运动速度的增大，液滴的最大铺展直径和达到最大铺展直径的时间增加，这是固体表面给液滴施加的额外能量造成的。

2.1.2铺展速度

图5所示为具有不同物性和撞击速度的液滴的U*随t*的变化。液滴撞击静止固体表面时，铺展速度在撞击后短时间内达到最大值，然后在黏性力和表面张力的作用下，铺展速度减小至0，并达到最大铺展；随后液滴开始回缩，但速度远小于初始铺展速度。在图5(a)中，黏度较大的液滴在铺展和回缩过程中受到的阻力较大，铺展和回缩速度均较小。如图5(b)所示，表面张力较大的液滴在铺展时受到的阻力较大，在回缩时动力较大，此时产生较小的铺展速度和较大的回缩速度。如图5(c)所示，撞击速度较大的液滴具有较大的初始动能，克服黏性力和表面张力之后的剩余能量较大，在铺展和回缩时均具有较大的速度。

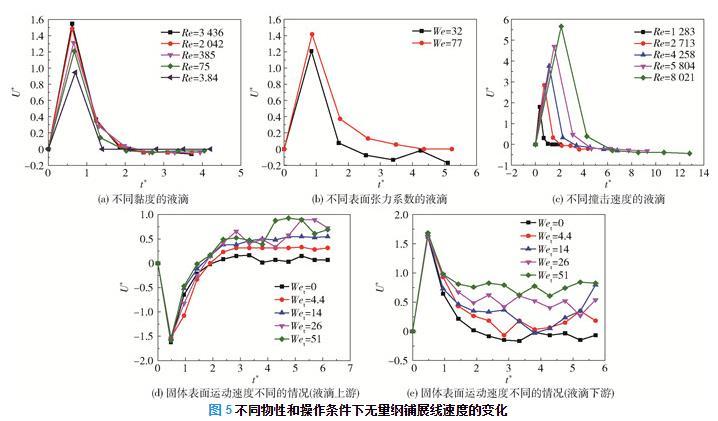
图5不同物性和操作条件下无量纲铺展线速度的变化

在固体表面水平运动时，定义液滴上游方向为液滴铺展与固体表面运动相同的方向，反之为液滴下游方向。如图5(d)所示，液滴上游铺展线速度(绝对值)在撞击后的短时间内增加到最大值，但由于其方向与固体表面运动方向相反，随着固体表面运动速度的增大，液滴受到的黏性力增大，且上游铺展线速度降低。液滴上游铺展线速度降至0之后，黏性力与上游铺展线速度的方向开始相同，此时黏性力作正功，因此固体表面运动速度的增大会使得上游铺展线速度增大，直至上游铺展线速度与表面运动速度相等。如图5(e)所示，在撞击的瞬间，液滴下游铺展线速度大于表面的运动速度，此时黏性力做负功，且下游铺展线速度会逐渐减小至固体表面运动速度。

2.1.3最大铺展直径

最大铺展直径Dmax是液滴撞击固体表面过程中的重要参数，定义相应的液滴最大无量纲铺展因子如式(8)所示

$D_{max}^{*}=frac{D_{max}}{D_{0}}$(8)

表3为文献中几个关于液滴最大无量纲铺展因子的关联式。将这些文献中的Dmax*计算值与本文实验中的结果进行对比，结果如图6所示。液滴撞击在玻璃表面上，而在本文实验中液滴撞击在不锈钢固体表面上，由于玻璃表面的润湿性较好，液滴撞击在其上的铺展直径较大，因此使用由实验结果拟合而得的式(9)计算的Dmax*大于本文实验值，平均误差约为20%。在计算黏性耗散时仅考虑了边界层内的黏性耗散，使得其计算值较小，而本文采用能量法时认为有更多的能量转化为了表面能，计算所得的Dmax*大于实验值，平均误差约为20%。在3 < Re < 9000，27 < We < 300时，由式(11)[17]计算所得的Dmax*与实验值的平均误差约为15%。当75 < Re < 9000，27 < We < 300时，由式(12)[18]计算所得的Dmax*与实验值的平均误差约为15%。在0 < We < 40，0 < Wet < 51时，由式(13)[19]计算所得的液滴撞击运动固体表面的Dmax*与实验值的误差小于15%。

表3最大无量纲铺展因子的不同模型

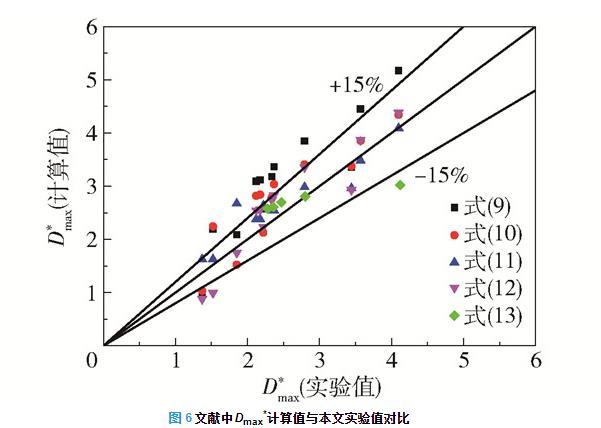
图6文献中Dmax*计算值与本文实验值对比

2.2铺展面积

不同物性和操作条件下无量纲铺展面积的变化如图7所示。可以看出，铺展面积随时间变化的一般趋势为先增大后减小。随着黏度的增大，或表面张力的增大，或撞击速度的减小，液滴的铺展面积和最大铺展面积均减小。当液滴黏度过大或撞击速度过小时，其铺展面积始终小于液滴的初始表面积；而当液滴表面张力系数较小或撞击速度较大时，其最终铺展面积大于液滴的初始表面积。

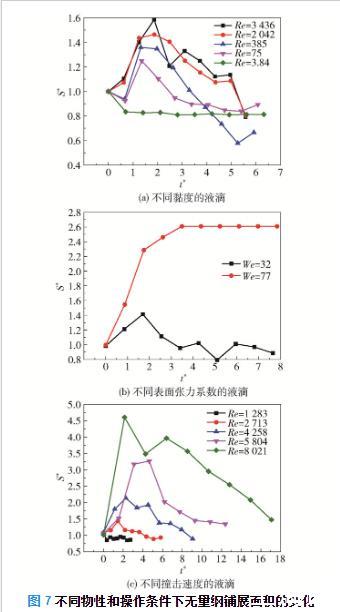
图7不同物性和操作条件下无量纲铺展面积的变化

假设液滴撞击固体表面后达到最大铺展时近似形成圆柱状，根据式(14)可计算液滴的Smax*

图8为文献中Smax*计算值与本文实验值对比。将式(9)~(12)代入式(14)求得的Smax*与实验值的平均误差分别约为30%、30%、20%和20%。这是由于液滴至最大铺展时的形状并不是严格的圆柱，其实际铺展面积小于相应的圆柱，则将液滴至最大铺展时的Smax*形状认为是圆柱形并根据式(14)计算得到的值大于实验值。

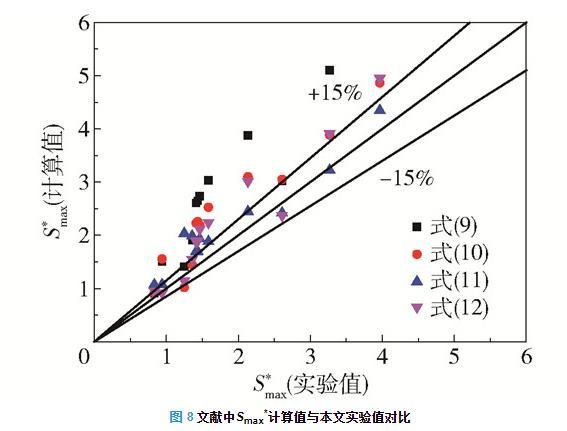
图8文献中Smax*计算值与本文实验值对比

对Smax*的实验值进行拟合，得到Smax*关于Re和We的关系式如式(15)所示

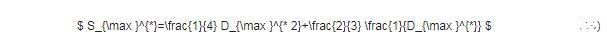
$ S_{\max }^{*}=0.203 R e^{0.064} W e^{0.43} $ (15)

图9为Smax*实验值与式(15)的Smax*计算值的对比，式(15)的Smax*计算值与实验值误差在大部分情况下都小于15%，因此在75 < Re < 9000，7 < We < 300时，可使用式(15)预测液滴撞击不锈钢固体表面的最大铺展面积。

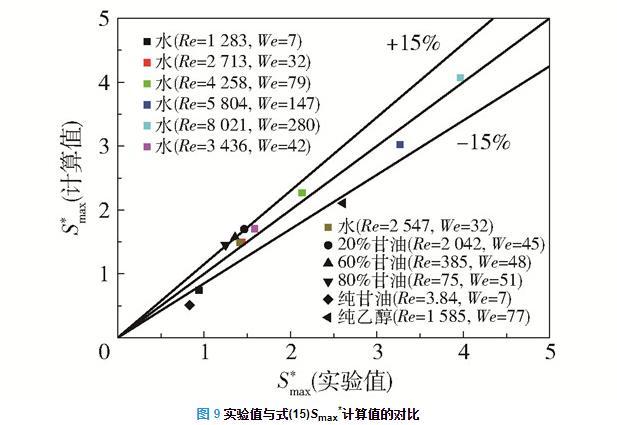
图9实验值与式(15)Smax*计算值的对比