合作客户/
拜耳公司 |
同济大学 |
联合大学 |
美国保洁 |
美国强生 |
瑞士罗氏 |
相关新闻Info
-
> 表面张力尺度效应对微纳米器械的制造有指导意义
> 石油磺酸盐中有效组分的结构与界面张力的关系
> 定性分析聚合物界面张力与系统黏度比之间的关系——数值仿真结果、结论
> 秦汉时期的物理学研究成果
> 碱性淀粉酶的异源表达及分子改造
> 表面活性素制备、分离纯化、溶液表面张力测定及胶束化行为研究(二)
> LB法组装Silicalite-1型分子筛晶粒层,制备出高度b-轴取向的ZSM-5分子筛膜
> 基于界面张力仪和电位仪分析SPF减水剂结构-性能关系(二)
> DHSO、AGE、TMHC构建阳离子有机硅表面活性剂DAT防水锁性能(一)
> 利用具有较强的表面张力的羧酸改良氧化铅锌矿球团干粉成型粘合剂
推荐新闻Info
-
> 界面张力主导:残余气饱和度的深部咸水层CO2封存潜力评估(三)
> 界面张力主导:残余气饱和度的深部咸水层CO2封存潜力评估(二)
> 界面张力主导:残余气饱和度的深部咸水层CO2封存潜力评估(一)
> 两类农用防雾涂层表面张力的深度计算与比较分析(二)
> 两类农用防雾涂层表面张力的深度计算与比较分析(一)
> 药液表面张力、喷雾方法对雾滴在水稻植株上沉积的影响(三)
> 药液表面张力、喷雾方法对雾滴在水稻植株上沉积的影响(二)
> 药液表面张力、喷雾方法对雾滴在水稻植株上沉积的影响(一)
> 烷基二苯醚/烷基苯混合磺酸盐静态表面张力、金属腐蚀性及净洗力测定(二)
> 烷基二苯醚/烷基苯混合磺酸盐静态表面张力、金属腐蚀性及净洗力测定(一)
液滴撞击固体表面过程中黏度与表面张力系数变化(三)
来源:北京化工大学学报(自然科学版) 浏览 945 次 发布时间:2025-01-13
2.3撞击过程中液滴的能量
液滴撞击固体表面的过程中,若忽略势能的变化,能量在动能、表面能、黏性耗散三者之间转换。设液滴的初始表面能为ES0,初始动能为EK0,液滴在撞击后任意瞬间的表面能为ES,动能为EK,黏性耗散为EV。此时,有关系式
图10为不同物性和操作条件下液滴表面能的变化。由图4(a)、图7(a)和式(19)均可得到液滴铺展直径和铺展面积随时间先增大后减小的一般规律,且随着黏度的增加,液滴的铺展直径和铺展面积均减小,液滴表面能增加的速率也在降低。
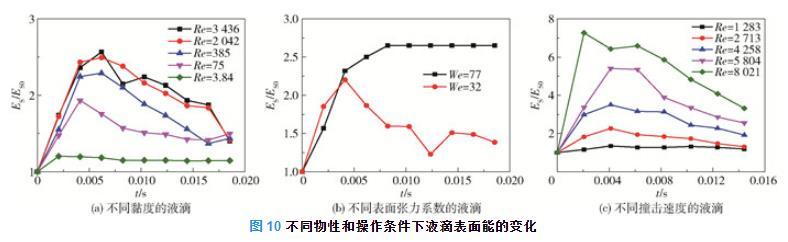
图10不同物性和操作条件下液滴表面能的变化
表面能随着表面张力系数的减小而减小,表面张力系数较小时液滴的铺展面积较大,表面能的增加量较大,且由于其不发生回缩,其表面能达最大值后保持不变。随着表面张力系数的增加,在撞击的初始阶段液滴表面能增加的速率变大。
由图4(c)、图7(c)和式(19)均可知,随着撞击速度的增加,液滴铺展直径和铺展面积增加,从而带来液滴的表面能增加量的增大。此外,随着撞击速度的增大,铺展过程中液滴表面能增加的速率变大。
2.3.2动能
因仅使用高速相机无法获取液滴内每个质点的速度,故使用液滴质心的速度计算液滴动能,如式(21)所示。
式中UC为液滴质心的速度。
图11(a)显示出具有不同黏度的液滴的动能随时间先减小后增大的一般趋势。在撞击的初始阶段液滴动能减小的速率最大,随着黏度的增加,液滴在铺展过程中动能减小的速度加快,说明随着液滴黏度的增大,有更多的动能耗散在黏性中。
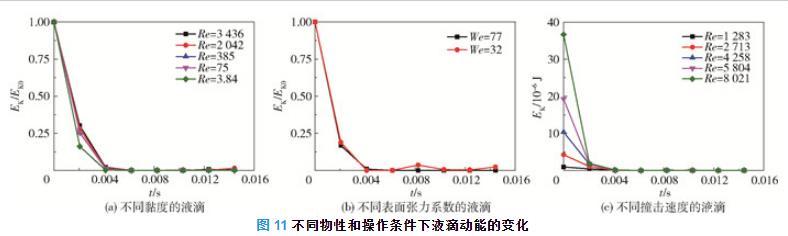
图11不同物性和操作条件下液滴动能的变化
图11(b)为水和乙醇液滴在撞击过程中动能随时间的变化。可以看出,液滴在铺展过程中动能的减小量和减小的速率不随表面张力系数而变化。
图11(c)为不同撞击速度下液滴动能随时间的变化。随着撞击速度的增加,液滴在铺展过程中动能减小的速度增大。撞击速度较大的液滴初动能较大,在表面张力和黏性力的作用下剩余能量更多,动能较大;并且撞击速度较大的液滴受到的黏性力较大,更多的动能耗散在黏性阻力中,致使其动能减小的速率增大。
2.3.3黏性耗散
可用式(22)计算液滴在撞击过程中能量耗散在黏性中的值

式中,Ux、Uy和Uz分别为液滴内流体在x、y和z方向的速度,但本文中无法获得液滴内部的速度分布以及速度的梯度随撞击时间的变化。液滴在撞击过程中能量耗散在黏性中的值可用式(23)计算
如图12(a)所示,具有不同黏度的液滴的黏性耗散占总能量的比例先增加后几乎保持不变。在撞击的初始阶段,液滴黏性耗散的速率最大。由图5(a)可知,当液滴的黏度增加1000倍时,液滴的铺展线速度减小为原来的0.61,液滴铺展线速度减小的程度远小于液滴黏度增大的程度,液滴内部速度梯度减小的程度远小于液滴黏度增大的程度,则根据式(22)可得液滴在撞击过程中的黏性耗散率和黏性耗散速率均随着黏度的增大而增大。
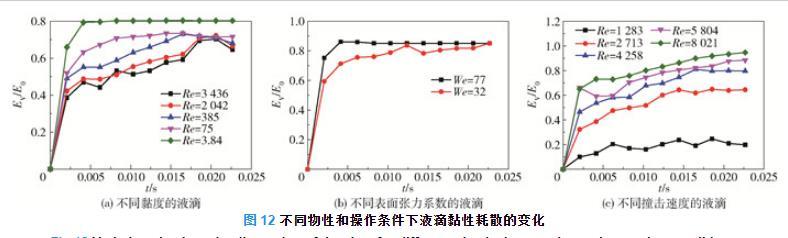
图12不同物性和操作条件下液滴黏性耗散的变化
图12(b)为水和乙醇液滴的黏性耗散随时间的变化。由图5(b)可知,当液滴的表面张力系数减小为原来的0.31时,液滴的铺展线速度增加1.18倍,液滴内的速度梯度相应也有所增加,则根据式(22)可得乙醇黏性耗散速率大于水液滴黏性耗散速率。
图12(c)为液滴在不同撞击速度下的黏性耗散情况。由图5(b)可知,液滴的撞击速度增加6.25倍时,液滴的最大铺展线速度增加3.14倍,液滴内部的速度梯度增加,则根据式(22)可得液滴在撞击过程中的黏性耗散率和黏性耗散速率均随着撞击速度的增大而增大。
2.3.4能量的计算
液滴的撞击过程与质量-弹簧-阻尼系统类似,因此建立液滴撞击的弹簧阻尼模型,液滴的质量为m,初始直径为D0,铺展直径为D,弹簧的弹性系数为k(N/m),阻尼器的阻尼系数为c(kg/s),根据牛顿第二定律可得

式中,h为液滴的铺展高度。
可根据式(19)、式(1)、式(26)~(28)计算液滴表面能。由式(26)可求得液滴的铺展线速度进而求得液滴的动能。根据以上求得的液滴表面能和动能以及式(16)可求得液滴的黏性耗散。
图13为液滴直径和能量的计算值与实验值对比。可以看出,液滴直径的计算值和实验值的平均误差约为15%(图13(a)),液滴表面能的计算值和实验值的平均误差约为15%(图13(b)),液滴动能的计算值和实验值的误差较大,最大误差约为50%(图13(c)),液滴黏性耗散的计算值和实验值的误差小于15%(图13(d))。
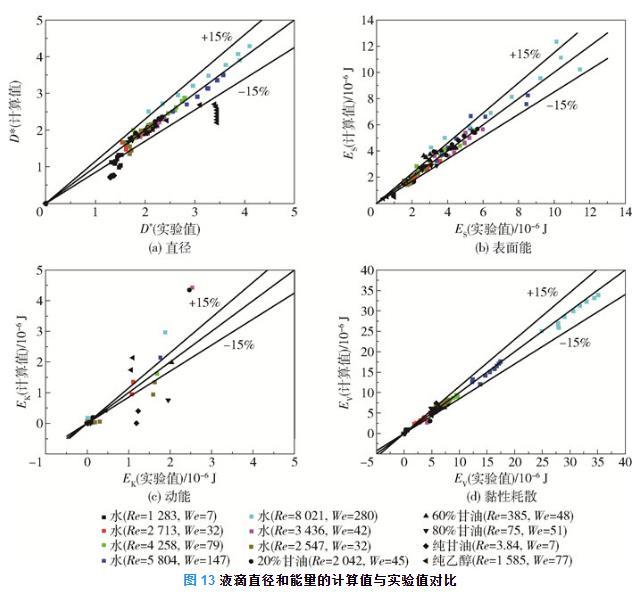
图13液滴直径和能量的计算值与实验值对比
3结论
(1)铺展直径和铺展面积随时间变化的一般趋势为先增大后减小,铺展线速度随时间变化的一般趋势为先在短时间内增加到最大值,随后逐渐减小到0。随着液滴黏度的增加,或表面张力的增大,或撞击速度的减小,液滴的铺展直径、铺展速度和铺展面积均减小。
(2)在75 < Re < 9000,7 < We < 300时,可使用关系式Dmax*=We14和Smax*=0.203Re0.064We0.43分别预测液滴的最大铺展直径和最大铺展面积。
(3)在液滴撞击的过程中,其表面能变化的一般趋势为先增大后减小,其动能变化的一般趋势为先减小后增大,其黏性耗散变化的一般趋势为先增大后保持不变。能量在黏性中的耗散主要发生在撞击的初始阶段。随着液滴黏度的增加,或表面张力系数的减小,或撞击速度的增加,黏性耗散的速率均增加。










