强子夸克相变的表面张力

对于一级相变，当体系的温度达到相变临界温度时，模型的热力学势能具有两个相等的极小值，并且这两个极小值被一个势垒分开。此外，由图1可知，这两个极小值所对应的σ场的真空期望值分别对应一个大的数值和一个小的数值。如果体系的温度进一步降低，那么σ期望值较小的那个真空势能将大于σ期望值大的那个真空势能，此时我们把前面那个真空称为亚稳态真空（通常称为伪真空），而把后面那个真空称为稳定真空（通常称为真真空）。

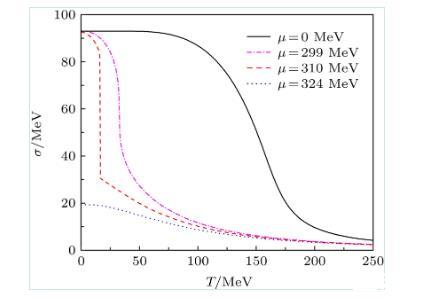
图1在不同夸克化学势密度条件下,σ场的真空期望值随温度的演化行为

在经典物理中，虽然伪真空的能量高于真真空，但是由于两个真空之间还有一个势垒，故伪真空无法回到真真空。但是，对于一个量子体系，由于存在量子隧穿效应，伪真空还有一定的概率可以回到真真空，从而发生一级相变，并把多余的能量以相变潜热的形式释放出来。为了准确地描述该一级相变的相变动力学过程，我们借助液滴核合成唯象模型来描述夸克强子的一级相变。

在液滴核合成唯象模型中，由于存在涨落，会产生一系列新的、能量较低的真真空的泡泡（通常用一个球形泡泡来模拟强子相），然后通过这些泡泡的膨胀最终实现从伪真空到真真空的转变。具体的完成过程如下：由于伪真空的单位体积自由能密度高于真真空的单位体积自由能密度，泡泡在膨胀的过程中，体系的能量降低，但是，由于这些泡泡同时存在表面张力，又会束缚气泡的膨胀，二者存在竞争关系。体积自由能与r3成正比，表面自由能与r2成正比，故存在一个临界半径rc,当r<rc时，表面自由能占主导地位，泡泡会最终收缩为伪真空，从而消失；而对于r>rc,体积自由能占主导地位，泡泡会一直膨胀直至占据整个系统，从而完成夸克相到强子相的完全转变。

如果把真真空的泡泡看成是一个半径为r的球形泡泡，那么体系总自由能的改变为

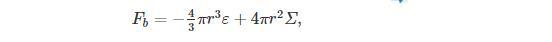
其中，ε为伪真空与真真空的单位体积自由能密度之差；Σ是泡壁的表面能量密度，即两相界面的表面张力。

在伪真空的环境下，大小不一的真真空泡泡，由于量子涨落和热涨落随机出现并消失，直至泡泡的半径大于等于临界半径，然后这些泡泡就会一直膨胀下去，完成一级相变的相变过程，并把多余的体系自由能以相变潜热的形式释放到环境中。基于这个机制，单位时间单位体积的临界泡泡成核率可以表示为

其中，T为系统温度。因子P通常比较难计算，为了计算方便通常采用简单的量纲分析，用T4近似代替P.利用欧几里得空间的有限温度场论方法，上述的成核率可以从下面的欧几里得拉格朗日密度出发：

这里为了方便讨论，我们把热力学有效势能重新定义为Veff（σ）=Ω（σ,T,μ）。则体系的自由能表示为

为伪真空下的σ场的真空期望值。也就是说，远离真真空泡泡的中心，体系处于亚稳态，相当于真真空的泡泡在伪真空中产生并膨胀。

对于一般有效势Veff,在边界条件（16）式下，通常不能通过解析方法得到（15）式的解析解，只能求助计算机得到该方程的数值解。但是，如果考虑真真空泡泡的尺寸比壁厚大得多的情况，或者伪真空与真真空的势能差与介于两个真空之间的势垒相比小得多的情况，该情况也称为薄壁（thin-wall）近似，则方程式（15）中的第二项与第一项相比可以被忽略，即方程进一步简化为由此，一旦得到了体系的自由能Fb,就可以很容易估算出夸克强子一级相变的成核率Γ.

利用薄壁近似，图2给出了当T=Tc时，夸克强子一级相变的表面张力随夸克化学势的变化。可知在一级相变区域，当化学势增大时，强子相的表面张力也随着化学势增大。当温度接近零时，强子夸克相变的表面张力约为12.6 MeV/fm2.在T→0的情况，本文理论预言与文献一致，但该文献只是考虑T=0的冷夸克物质的夸克强子一级相变。

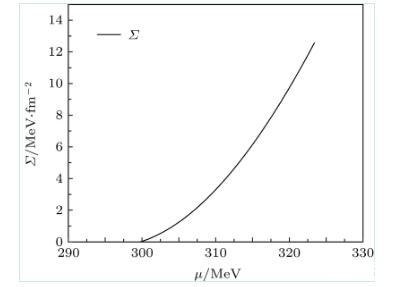
图2 T=Tc时表面张力与夸克化学势的演化关系

结论

利用两个夸克味的夸克介子模型，在有限温度、有限夸克化学势密度条件下，本文计算了模型热力学有效势能，通过求解该热力学有效势能对σ场的变分，得到σ介子场的运动方程，求解该运动方程得到σ场的真空期望值随温度和密度的变化关系。我们发现，在高温低密度区域，量子色动力学的相变是过渡相变，而在低温高密度区域，量子色动力学的相变是一级相变，在过渡相变和一级相变的交界处存在一个相变的临界点，我们称之为CEP（critical end point）。为了提供更加完整的理论结果，不同于其他文献，我们在模型的计算中考虑夸克场的真空涨落和重整化效应，并且我们采用了一套广泛应用并被实验认可的模型参数来计算。特别是夸克场的真空涨落效应，通常会使得一级相变的相变区域变得很小，从而进一步推低夸克强子相变的强子相的表面张力的数值，而很小的表面张力数值，使得中子星在早期演化过程中产生更加复杂的中子星结构，比如中子星的混合相的出现，夸克星硬层的出现等物理现象。

考虑到基于夸克介子模型的热力学性质计算结果与当前的格点量子色动力学计算差距较大，与当前的实验观测也有相当大的出入，故在该模型中我们考虑胶子的自由度，把夸克介子模型进一步推广到Polyakov圈拓展的Polyakov-quark-meson model（PQM）模型。由于考虑了Polyakov圈拓展，需要在模型中引入另外两个序参量，因此PQM模型具有三个序参量，在计算夸克强子相变表面张力时，需要同时求解三个非线性微分方程组，理论和数值计算将变得非常复杂和困难，特别是在这种情况下，薄壁近似将不再有效，只能采用数值计算来获得表面张力的数值信息。目前，该方向的研究正在进行中。