准确预测盐水-气体界面张力对于优化储层中气体的分布和运移至关重要。这有助于减少气体泄漏风险、提高储存容量，并保障地下气体储存的长期稳定性，同时推动清洁能源发展和减少碳排放。然而，目前预测界面张力的方法（如实验法）存在耗时、费力、成本高以及难以表征多组分气体共同影响的问题。此外，在盐水-多组分气体（如H2，CH4,CO2等）界面张力方面，缺乏准确的数学表达式。

近年来，机器学习算法显示出了良好的预测潜力。在众多机器学习方法中，自动机器学习（AutoML）算法可处理具有多个因素的复杂预测任务，适用于盐水-多组分气体界面张力的预测问题。符号回归（SR）可通过数据生成相应的数学表达式，从而为机器学习模型提供可解释性。然而，这两种方法在训练和发现过程中非常耗时，需要一种先进的算法来提高效率。遗传算法（GA）是一种生物启发式算法，具有高效的全局搜索能力，可用于解决优化问题，从而提高模型开发和应用的效率。

因此，本文提供了一中基于遗传算法优化的自动机器学习和符号回归模型（GA-AutoML-SR），以准确预测盐水-气体界面张力，并生成相应的数学表达式。

遗传算法优化的界面张力智能预测方法

采集原始数据，并对所述原始数据进行归一化，得到归一化数据；

初始化自动机器学习模型的候选模型集合，所述候选模型集合包括多个候选机器学习模型；

定义遗传算法的参数；

从所述候选模型集合中选择第一数量的候选机器学习模型，作为个体；

基于所述归一化数据，对每个所述个体的第一预测结果进行性能评估，得到每个所述个体的选择概率；

根据所述选择概率，构建累积序列，并基于所述累积序列，确定被选个体；

设置所述被选个体的数量加1，并判断所述被选个体的数量是否小于第二数量，若是，跳转至从所述候选模型集合中选择第一数量的候选机器学习模型步骤；若否，对所述被选个体进行变异，得到变异后个体；

基于所述变异后个体，进行个体间交叉，生成后代个体；

第一迭代次数加1，并判断第一迭代次数是否小于第一迭代阈值，若是，跳转至从所述候选模型集合中选择第一数量的候选机器学习模型步骤；若否，将当前所述后代个体作为预测模型；

基于所述原始数据，生成多组样本数据，并对所述样本数据进行归一化，得到归一化样本；

将所述归一化样本输入所述预测模型，得到第二预测结果；

将所述第二预测结果和所述归一化样本作为补充数据集，合并所述补充数据集和所述归一化数据，得到合并数据；

定义表达式算子；

基于符号回归，根据所述表达式算子和所述合并数据，生成初始模型表达式；

利用遗传算法搜索所述初始模型表达式的空间，确定候选表达式；

对所述候选表达式的适应度进行性能评估，搜索得到最优的模型表达式。

可选地，基于所述归一化数据，对每个所述个体的第一预测结果进行性能评估，得到每个所述个体的选择概率，具体为：

将所述归一化数据作为所述个体的输入，得到所述个体的第一预测结果；

采用适应度函数对所述第一预测结果进行性能评估，得到对应个体的适应度值；

可选地，根据所述选择概率，构建累积序列，并基于所述累积序列，确定被选个体，具体为：

顺序排列所有个体的选择概率，形成第一集合；

将第一集合中的当前值与累积序列中对应位置的前一个值的和，作为累积序列的当前值；

选择介于0到1之间的一个值，作为判定值；

将所述累积序列中与所述判定值的距离最近的数值，作为所述被选个体。

可选地，对所述被选个体进行变异，得到变异后个体，具体为：改变所述个体的结构或参数。

可选地，基于所述变异后个体，进行个体间交叉，生成后代个体，具体为：

分别从各个变异后个体中提取特征进行组合，生成新的特征集，作为后代个体的特征表示，得到所述后代个体。

可选地，基于所述变异后个体，进行个体间交叉，生成后代个体，具体为：

将各个变异后个体的参数进行组合，得到新的参数，对所述新的参数进行训练，得到所述后代个体。

可选地，基于所述变异后个体，进行个体间交叉，生成后代个体，具体为：

将一个变异后个体的分部，结合到另一个不同的变异后个体的决策边界中，创建具有新结构个体，作为所述后代个体。

可选地，对所述候选表达式的适应度进行性能评估，搜索得到最优的模型表达式，具体为：

基于所述合并数据，对每个所述候选表达式的第三预测结果进行性能评估，确定被选表达式集合；

对所述被选表达式集合中的所有被选表达式进行变异，生成变异表达式；

基于所述变异表达式，进行交叉，生成后代表达式；

最终得到具体模型表达式为：

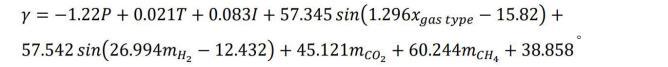
基于遗传算法优化的自动机器学习和符号回归模型融合遗传算法、自动机器学习和符号回归方法，进行界面张力的预测，相较于传统实验测量方法，提高了界面张力的预测速度和精度，同时通过数学表达式提高了数据驱动模型的可解释性。