合作客户/
拜耳公司 |
同济大学 |
联合大学 |
美国保洁 |
美国强生 |
瑞士罗氏 |
相关新闻Info
-
> 筛选常用、经济且可抑制低阶煤煤尘的表面活性剂(三)
> 表面张力和接触角的关系(Young方程表达式)
> 裂缝性水封气藏解封过程中润湿反转剂浓度、气水界面张力变化(一)
> Delta-8 动物胃肠道体内中药物的溶解度的测定——结论、工具书类!
> 温度对水—十二烷基硫酸钠体系与纯水体系界面张力、厚度的影响——结果与讨论、结论
> 不同温度和压力对AOT稳定CO2乳液的界面张力影响(二)
> 塑料件二次加工如何改变表面张力?
> 为什么葡萄酒会从下部往杯子的上部走呢?
> 基于表面张力等分析油酸钠体系下磁化处理对赤铁矿和石英浮选分离效果的影响
> 酚胺树脂聚醚型破乳剂分子结构、浓度对油-水界面张力的影响——实验部分
推荐新闻Info
-
> 影响狭缝间氢键流体气液平衡界面张力的因素有哪些(三)
> 影响狭缝间氢键流体气液平衡界面张力的因素有哪些(二)
> 影响狭缝间氢键流体气液平衡界面张力的因素有哪些(一)
> GA、WPI和T80复合乳液体系的脂肪消化动力学曲线、界面张力变化(四)
> GA、WPI和T80复合乳液体系的脂肪消化动力学曲线、界面张力变化(三)
> GA、WPI和T80复合乳液体系的脂肪消化动力学曲线、界面张力变化(二)
> GA、WPI和T80复合乳液体系的脂肪消化动力学曲线、界面张力变化(一)
> 表面张力实验、接触角实验分析抑尘试剂对煤的润湿结果
> Kibron表面张力仪研究烧结矿聚结行为
> 基于界面张力和表面张力测试评估商用UV油墨对不同承印纸张的表面浸润性差异(三)
探索界面张力梯度驱动对流转捩规律
来源:力学进展 浏览 774 次 发布时间:2024-07-05
界面张力梯度驱动对流是空间自然对流热质输运的基本形式,对其时空转捩过程、转捩机制、非线性特征及流动向湍流转捩途径等基本规律的研究,一方面可以丰富非线性动力学的相关理论,另一方面对于人类认识、探索和利用空间环境也具有重要的应用价值,是微重力流体物理的重要研究内容和学科前沿。本文对目前的研究现状进行了总结,重点介绍了研究液层界面张力梯度驱动对流的实验及数值模拟方法,虽然已有的研究已经得到在不同模型和工况下的各种转捩模式,但是在转捩规律上仍需要更深入的探索,可以从以下几个方面着手:
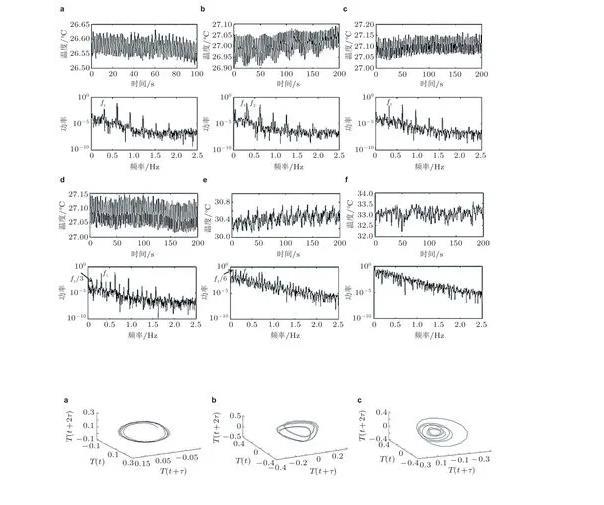
(1)理论分析和数值模拟结果的正确性需要由实验来验证,空间实验可以满足微重力环境、长时间观测的要求,但是空间实验有一定难度且机会来之不易,故而可以考虑进一步发展实验手段,以实现数值模拟中采用的更丰富的工况;以及加强对实验条件的控制,以降低无关因素的干扰,提高实验精度。
(2)目前关于液层界面张力梯度驱动对流向湍流的超临界转捩在数值方法上主要有流动时序数据的分析和分岔问题的数值算法。流动宏观量的时序数据来自实验结果或者直接数值模拟,对于后者,需要对于不同参数分别进行数值模拟,再通过时间序列频谱及其混沌特性的定量计算分析流动转捩规律,即在大量的离散的数据序列中寻找分岔点,故此过程比较繁琐。而通过构造分岔方程对分岔进行数值计算的方法虽然可以一步到位,但是在选取分岔方程,解高维线性、非线性方程等过程中均需要根据具体的流动模型进行调整,具有一定难度,且对于更加复杂的流动模式需要更大的计算量,用此算法也无法直接计算得到混沌解。上述两种方法各有优缺点,目前在转捩过程的数值研究中较为常用的仍是在不同参数下进行直接数值模拟,而后对大量数据进行频谱分析,识别分岔点;在直接对分岔进行数值计算的研究中,也常常需要通过直接数值模拟来验证分岔得到的解的可靠性与准确性,在今后的研究中可考虑进一步将两种方法结合运用,互相补充、验证。
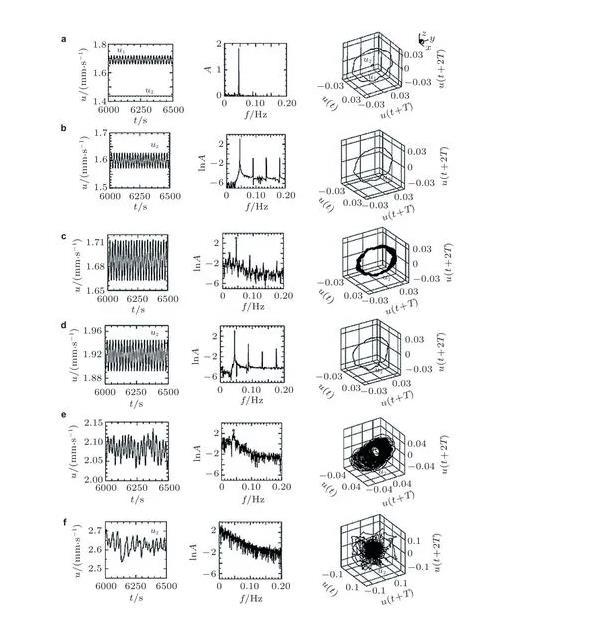
(3)液层界面张力梯度驱动对流向湍流转捩的过程中会产生丰富的流动模式,转捩过程除了与上文提到的液层模型、无量纲参数(Prandtl数、高径比、体积比等)有关,还受到热边界条件(如体系是否绝热)、加热方式及加热速率等因素的影响;此外,在具体的应用场景中通常有多种流动相互作用,考虑界面张力梯度驱动对流与其他诸如浮力、电磁场、旋转等效应的耦合,对于重新检视已发现的转捩途径以及寻找新的转捩途径均有一定的积极意义。
(4)目前对于液层界面张力梯度驱动对流向湍流转捩的研究仍不够完善,在对超临界转捩阶段的实验及数值模拟研究中观察到了许多复杂的转捩模式,但大多只是现象上的描述,并未总结出普遍的规律;对于流动最终能否通向混沌暂无普适的判据,流动通向混沌过程中出现的诸如阵发、锁频等特殊的现象也尚未有更本质的机理上的解释。总之,对于转捩规律的深入理解,需要界面张力梯度驱动对流这一非线性模型在理论上的进一步发展,未来道阻且长。










