2界面张力模拟近似计算

在悬浮床加氢体系中，原料油的界面张力的大小直接影响体系中气泡的大小和分布范围及尺寸大小，这对于体系中气体如H2从体相向催化剂表面、油品表面的扩散有很大的影响，随着温度的变化，其界面张力也呈现出不同的变化规律。因此，计算工况条件下渣油在H2气氛下的界面张力变化对于建立渣油悬浮床加氢气泡尺寸模型尤为重要。

但是，目前关于气体/渣油界面张力的研究集中在CO2/N2等气体驱油的领域中，关于加氢领域中尤其是H2气氛下渣油的界面张力研究还处于空白状态。因此，本文主要以与H2分子结构较为相似的N2为主要研究考察對象，考察N2气氛下渣油的界面张力。另外，对于不同气氛下的渣油的界面张力变化来说，气体的沸点越低，其在高压下溶解入渣油之中导致界面张力变小的幅度变化越小。

查表可知，在标准状态下，CO2沸点-56.5℃，N2沸点-195.6℃，H2沸点-252.7℃，因此，相同压力下，H2气氛下降低的幅度应该比N2气氛相对应的界面张力下降幅度小，因此，可以得到在高压条件下的H2/渣油的界面张力应当处于该渣油在N2气氛下常压以及高压条件下界面张力之间。

根据上述分析，并考虑到在较高温度下渣油组成的剧烈变化导致的计算偏差情况，可以计算得到N2在常压条件下以及高压条件下的界面张力，从而对H2在高压条件下的界面张力进行限定。

2.1 N2气氛常压条件下的界面张力计算

首先，界面张力的模拟计算与油品的馏程等有很重要的关系，需要通过油品的平均沸点等数据，可以根据油品的蒸馏曲线得到的平均沸点数据。体积平均沸点，是平均沸点的表示方法之一，是恩氏蒸馏10%、30%、50%、70%、90%五个馏出温度的算术平均值。用于求定其他物理常数。

由于减压渣油过重，超过质量分数80%的油品在实际操作过程中是无法馏出，这给计算油品的平均沸点造成了困难。考虑到目前得到的油品蒸馏曲线均为典型的S型曲线，因此将现有曲线采用Boltzmann计算模型来进行模拟拟合。

通过Boltzmann计算模型得到的红色拟合曲线的相关性Adj R2=0.999 76≈1，说明拟合曲线拟合优度非常好，基本可以用拟合曲线作为真实蒸馏曲线得到平均沸点数据。

有研究者提供了一种利用原料油各项可测理化参数进行空气气氛、常压条件下界面张力估测的方法，在实际应用中被证明具有较高的准确度，本研究将以此为基础得到最初的界面张力数据，随后进行接下来的计算近似。

根据表一提供的Toledo减渣的物性数据，以及得到的减压渣油的模拟蒸馏曲线，可得到Toledo减渣特性因数为11.6，真临界温度为760℃，据此查表计算可得在常压、较高温度条件下常压条件、N2气氛下Toledo减渣的气液界面的界面张力，逐点计算后将结果汇总。

可以看到，根据文献方法计算结果，对于Toledo减压渣油来说，其在常压条件下N2气氛条件下的气液界面的界面张力，当不在真临界温度（760℃）较近的温度范围内，都可以认为随温度呈现线性下降的趋势。

对于接近真临界温度范围后的界面张力的变化，多篇文献报道了较较低温度范围斜率更低的线性变化关系，直至在真临界温度条件下，气液两相体系最终演变为气液部分体系，此时体系的不存在界面，则显然界面张力数据为零，与计算结果趋势一致。

2.2 N2气氛高压条件下的界面张力估算

在较高压力条件下，气液界面中气相一边的压力越大，气体分子从气相向液相中扩散的动力也就越大，最终导致一部分气体会溶解在渣油之中，由此导致气液界面的界面张力下降，一般来说，压力越高，溶解气体越多，气液界面的界面张力就越低。对于氮气来说，文献中报道了其在不同温度下的压力-界面张力关系，根据结果发现，在一定温度下，常压-20 MPa条件下的渣油界面张力与压力为线性下降关系。

可以发现，不同温度条件下渣油界面张力线性下降的斜率与温度存在较为明显的线性关系，即，温度越高，则气液两相界面张力随气相压力升高而降低的趋势则越小，且呈线性变化趋势。因此，根据此结果，可以以较低温度条件下的气液界面界面张力关系，推导在较高温度条件下的气液界面界面张力随外界条件的变化关系。

不同温度条件下的线性下降的斜率与温度的变化也基本呈现出一定的的线性。另外，对于不同压力下的界面张力-温度关系，理论上应当都是线性变化，因此，斜率变化的线性变化规律也是符合一般规律的。由此可以推测得到在相应温度条件下的线性下降斜率，从而由N2常压条件下Toledo减渣的界面张力推测得到N2在20 MPa气氛条件下Toledo减渣的界面张力。

综合上述分析，根据计算结果，黑色、红色分别为常压、20 MPa下N2与减压渣油的界面张力随温度变化的变化趋势，与文献规律吻合，均呈现线性变化规律。

对于根据前文对于不同气体在高压条件下气液界面的界面张力随温度变化的规律的推导，可知，H2气氛条件下其与减压渣油的界面张力随温度变化的规律曲线应处在N2常压以及20 MPa条件下的界面张力-温度两条曲线之间，即图中的黑色直线以及红色直线之间的阴影区域。

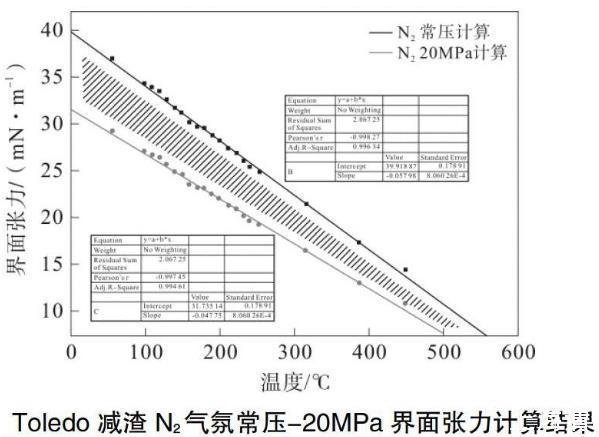
可以看到，对于本文给定的界面张力计算模拟的范围来说，同时考虑到数量级，误差基本可以控制在±3 mN/m范围内，另外考虑到计算过程的偏差，具有较大的准确性，这一结果具有一定的可参考价值。

3结论

本文建立了一种估算在较为苛刻的条件下，减压渣油在氢气气氛条件下的黏度、界面张力等随温度变化的关系的方法，在缺少相应的测量方法的条件下，可以对油品的相应参数进行简单的估算。

总体来说，油品的黏度、界面张力随着温度的变化都呈现出一定的变化规律，根据相关工作的经验性公式以及相关模型可以对于油品在工况条件下的黏温曲线以及界面张力进行一定程度的预测。对于界面张力计算模拟的范围来说，同时考虑到数量级，基本在±3 mN/m范围内，另外考虑到计算结果的误差性，这一结果基本可以参考;对于黏温关系来说，则存在数倍的差距，这一工作有实测工作的限制因素，以及工况条件下的减压渣油组成变化等因素的影响同时存在。

悬浮床加氢工艺条件下界面张力、油品黏度模拟近似计算（一）

悬浮床加氢工艺条件下界面张力、油品黏度模拟近似计算（二）