2.1.2无量纲分析

为了更详细地研究垂直电场对液滴铺展的影响，根据实验获得的连续照片分别测量了液滴演变过程中动态铺展直径L。图3(a)描述了无电场和三种不同模式下液滴的铺展因子α随无量纲时间τ的变化。液滴撞击后在短时间内扩散并且几乎同时达到最大铺展状态，随后液滴开始回缩，对应的铺展因子趋势下降，最后进入液滴振荡阶段，由于液滴和表面的钉住作用，铺展因子逐渐趋于稳定。从图3(a)可以看出，不同场强下的液滴在τ=1.19时达到最大铺展，并且最大铺展因子随着电场强度的增加而小幅度增大，这是因为分布在液滴表面上的同类自由电荷之间的库仑斥力会引入与表面张力相反方向的静电力，额外的静电力会减弱液体表面张力，进一步增强液滴的扩散。无电场与场强最大的液滴的最大铺展因子相差小于2%，说明在液滴铺展阶段，电场力不是主导影响因素，这与前人的研究结果保持基本一致。

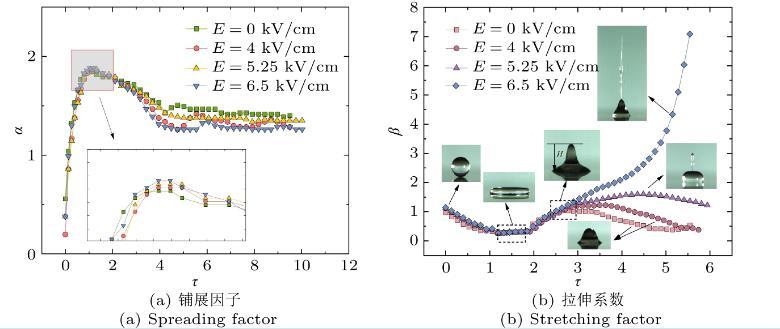
图3不同场强下液滴无量纲因子随无量纲时间变化(We=17.8)

当中性液滴落入电场并撞击带电表面后，该液滴会立即受到极化电荷的即时作用，导致其表面迅速获得电荷，同时会产生与撞击方向截然相反的强静电力，从而改变液滴在回缩过程中的形态。为了更清晰地观察液滴在电场中的回缩和拉伸过程，引入无量纲拉伸系数β，如图3(b)所示。在液滴铺展阶段，液滴的拉伸系数降低并在最大铺展时达到最低值，而电场强度的大小对此阶段液滴拉伸系数无明显变化，这是因为电场强度对液滴的铺展过程影响较小，这与图3(a)的实验数据一致。在τ=3之后，不同电场强度下的拉伸系数β趋势有了明显变化。随着电场强度的增加，即从模式一到模式三，液滴的拉伸系数显著增加。这是由于液滴在接触壁面后获得电荷且受到了随场强增大而增大的静电力。

2.1.3机理分析

在电场的施加下，电介质内部经历一个极化分子的移动和再排列过程，进而导致电荷分布重新组建，这个过程被定义为介电弛豫现象。而电荷在介质中达到稳定所需要的时间通常用时间常数τe来表示：

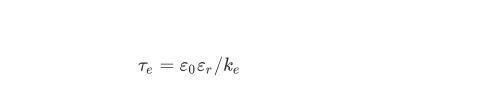(7)

式中，ε0为真空介电常数，εr为液体相对介电常数，ke为液滴导电率。本实验全程在空气常温环境下进行，此环境下去离子水(ke=5×10-6 S/m)的介电弛豫时间τe大约为在1.77μs，而液滴撞击过程维持了几十毫秒，远远大于介电弛豫时间，因此印证液滴在撞击过程中实现了充分的电荷积累，其撞击行为深受电流体力学影响。

液滴在撞击过程中受惯性力、重力、表面张力、静电力和粘滞力的共同影响。铺展阶段，惯性力占主导作用。而在拉伸阶段，惯性力和静电力促进液滴的拉伸，重力、表面张力和粘滞耗散抑制液滴拉伸，在力的共同作用下产生了图2的不同拉伸模态。在此过程中，由于电场是垂直方向，液滴的模态演化主要受到垂直方向力的影响，而水平方向受力作用较小，因此在后续分析中，我们假设水平方向受力变化对液滴形态的影响忽略不计，将重点分析垂直方向的受力情况，以此探讨不同拉伸模态的机理。

图4(a)为液滴顶端所受力的方向和液滴整体电荷分布。液滴接触下极板后，由于离子迁移和极化电荷的产生，中性液滴立即极化，其顶部带正电荷，底部带负电荷。根据库伦定律，电场方向垂直向上，作用在液滴顶部的静电力Fe是向上的，与电场方向相同，使液滴不断向上拉伸，液滴拉伸高度增加，而表面张力Fγ和重力G使液滴向下收缩。基于上述的分析，各个模态的产生机理均可通过静电力、表面张力和重力三者间的博弈关系来分析。三种作用力对液滴的影响大小可用局部静电应力pe、毛细应力pγ和重力应力pg来表示。静电力的大小由麦克斯韦应力张量T的散度给出，可表示为

图4液滴在不同模式下的动力学行为示意图

式中，rc为液滴顶点的曲率半径，h为液滴从顶部到底部的高度。pγ和pg均抑制液滴向上拉伸，为便于分析将上述两种应力定义为pγg=pγ+pg。因此，实验观察到的三种模态现象可以通过分析pe和pγg的竞争关系得到合理解释。第一模态中，pe/pγg远低于100数量级，此时表面张力占主导因素，静电力远不足以克服表面张力和重力的共同作用，只发生液滴拉伸现象。第二模态中，pe/pγg～100即处于同一数量级，在这种情况下，由于静电力、表面张力与重力三者之间达到了一个平衡状态，液滴顶部能够维持在一定的高度上，同时其颈部逐渐变得纤细，最终导致了断裂现象的发生。随着电场强度进一步增大，pe/pγg远超于100数量级，意味着静电力克服了表面张力和重力的约束，此时液滴顶部的曲率急剧增大，直至形成一个明显的尖端，进而使得液滴的整体形状趋近于一个圆锥体，这样的现象被称为“泰勒锥”。随着时间的推移，自由电荷会不断移动至液滴顶部尖端和周围空气界面的边缘区域进行累积，在此界面上，电场产生的切向静电力分量与流体运动过程中的粘滞力达到平衡状态，从而形成了稳定的锥射流，如图2(d)22 ms所示。在许多电喷雾实验中，都曾观察到这种喷射出细长细丝的现象，而这一现象正是静电纺丝领域所利用的关键过程。由于锥射流具有不稳定性：曲张不稳定性和扭结不稳定性。当射流电荷较低情况下，射流因受曲张不稳定性的影响而分裂成主液滴及其伴随的微小卫星液滴；在高电荷作用下，会出现扭结不稳定性破碎模式，促使射流破裂成大小不均的微小液滴。这两种不稳定性破碎模式均促使分裂出的小液滴带有正电荷，随后在电场的作用下迅速上升，同时残留的液滴顶部在表面张力作用下自然恢复到圆弧形态。

除此之外，液滴底部在不同模式下的动力学行为相同，如图4(b)所示。液滴底部会被诱导负电荷，此时其受到垂直向下的静电力Fel，静电力和粘附力Fa同时作用于液滴的底部，因此它们既不促进也不阻碍液滴的拉伸，其作用本质是使液滴附着在下极板上，防止其反弹。