液滴撞击固体壁面是一种常见的物理现象，广泛应用于喷墨打印、等离子喷涂、喷雾冷却、金属淬火和抑冰等领域。液滴与固体壁面的相互作用是影响上述应用的重要因素，如墨滴撞击纸张的铺展特性会影响喷墨打印的分辨率，液滴与壁面的接触时间会影响喷雾冷却的效率，而抑冰又要求减少液滴与壁面的接触时间。类似的情况还有许多，尽管很多学者已经开展了大量研究，但液滴与壁面的相互作用仍因其复杂性与多样性而未被全部知晓。

对于液滴撞击固体壁面，通常从两方面展开研究，即液滴的铺展特性与传热传质特性。学者们围绕这两方面进行了一定研究。随着越来越多的动力学及传热学特性被发现，研究工况的温度也随之升高，其中一个研究方向逐渐聚焦于高温情况下显著的液滴撞击特征，Leidenfrost现象。1756年，Leidenfrost提出了这一标志性的液滴撞击高温壁面特征，开创了新的研究领域。Leidenfrost现象是液滴受到高温壁面的影响，气液快速交换热量，液滴底部产生蒸汽膜的物理现象。蒸汽膜厚度受多种因素影响而不断发生变化，并存在程度不一的振荡情况。实验结果表明，Leidenfrost现象中液滴底部蒸汽为径向的层流流动，并有学者对蒸汽层的扩散提出了相关预测模型。

除底部气膜外，Leidenfrost现象下液滴的动力学与传热特性也与其它工况不同。首先，达到Leidenfrost状态需要有足够高的温度，这一温度通常被称为Leidenfrost点，其大小受到壁面粗糙度，重力和表面张力等因素的影响。其次，液滴撞击壁面的We数较大时，相对于未加热壁面与湿壁面，Leidenfrost状态下液滴更容易发生破碎。当液滴开始铺展时，由于液滴与壁面间的蒸汽膜存在，壁面粗糙度与接触角对液滴铺展的影响被削弱，这使得Leidenfrost状态下的液滴铺展情况大于膜态蒸发和核态沸腾状态下的液滴铺展情况，且液滴的最大铺展情况与脱离时间仍然由We数决定。

虽然，很多学者对Leidenfrost现象进行了一定研究，但是大部分研究成果聚焦于高温平面上的液滴动力学与传热特性，而非平面上Leidenfrost现象的研究非常有限。但是，液滴撞击高温曲面广泛存在于电子工程、机械工程、动力工程、化学工程等领域。如液滴撞击高温球面，常见于流化催化裂化和流化焦化等工艺，这一过程影响着多种过程系统的性能，尤其是对于生产更有价值的汽车燃料具有重要意义。鉴于此，本文进一步探究液滴与高温球面撞击过程中液滴的Leidenfrost现象，采用数值模拟方法进行研究，使用Fluent软件构建了二维轴对称数值模型，采用VOF模型及Lee模型，分析液滴撞击高温球面的动力学特性与传热特性，探讨Leidenfrost现象的机理及各因素的影响规律。

1.模型及方法

1.1物理模型

液滴撞击球面的物理模型如图1所示，半径为r的球状液滴以初速度v撞击半径为rn的固体球面，并在球面上铺展、收缩和反弹。液滴材料为水，考虑重力加速度的影响，液滴与壁面撞击时t=0.

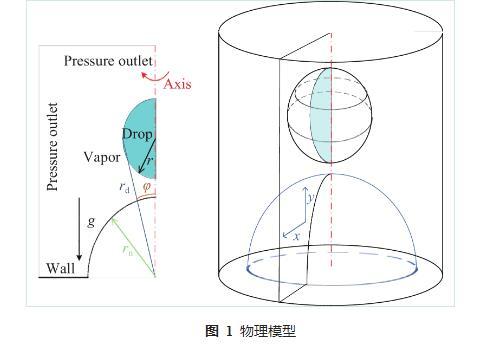
图1物理模型

定义无量纲系数铺展因子β

式中：rm为液滴铺展半径，mm.铺展系数β可以直观地反映液滴在壁面上铺展变化的规律。铺展系数越大，说明液滴铺展越充分。

与撞击平面不同，液滴撞击球面时会沿球面铺展，因此铺展半径rm的定义与平面有所不同

（2）

式中，φ为液滴铺展角度，rd为液滴铺展最大处与球心间的距离。

1.2控制方程

为了模拟液滴撞击热壁面的动力学行为，需要求解连续性方程、动量方程与能量方程，假设气液两相均为不可压缩流体，表面张力系数、密度、粘度、导热系数和比热等物性参数均为常数

式中，u为速度矢量；ρ为流体密度；S为相变引起的质量源项；μ是流体黏度；g为重力加速度；Fσ为表面张力；T为流体温度；Cp为定压比热；k为导热系数；Se为相变引起的能量源项。

1.3 VOF模型

VOF模型是一种两相流动计算模型，其通过计算网格中相的体积分数以捕捉两相的分界面，对于目标流体，流体体积函数C可表示为

流体体积函数满足的输运方程为

采用隐式格式求解流体体积函数方程，并包含隐式体积力，界面建模为sharp模型，采用的界面捕捉算法为Compressive方法。

两相流体的密度ρ、黏度μ、导热系数k的计算式为

式中，下标l、v分别表示液相和气相。

采用CSF模型计算表面张力，表达式为

式中，σ为表面张力系数；n为界面法向；κ为界面曲率。

1.4 Lee模型

本文采用Lee模型模拟气液相变过程，控制方程为

式中，αv为气相体积分数，uv为气相速度，

和为蒸发和冷凝的传质率。对于蒸发过程，传质表达式为

式中，αl为液相的体积分数；Tl为流体温度；Tsat为饱和温度；Acoeff为控制相变强度的因子，可以表示为

式中，db为液体蒸发时产生的气泡直径；χ表示液体表面吸附蒸气分子的量，为调节系数；M为摩尔质量；R为通用气体常数，8.314 J/（mol·K）；L为蒸发潜热；在本文中，Acoeff取值为500.

1.5网格无关性验证

为了选择合理的网格精度，首先开展网格无关性验证。同时，为了验证数值模拟的准确性，也需与实验结果进行对比验证。本文以文献中的工况为基准，采用异丙醇作为液相，展开网格无关性验证与模型验证。计算区域的尺寸为5 mm×8 mm,液滴初始温度为355.65 K、初始直径为1.61 mm、液滴撞击速度为0.348 m/s、We数等于8.6、球体直径为10 mm、壁面温度为623.15 K、壁面接触角为67°、重力加速度为−9.81 m/s2.其它流体物性如表1所示。

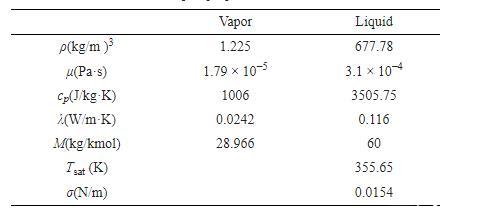
表1流体物性参数表

为了定量分析网格数量对数值模拟结果准确性的影响，以液滴撞击壁面时的铺展因子作为定量分析指标及网格无关性验证的评判标准。网格数量从36 w开始增加，每次增长大约30 w,并绘制液滴铺展因子β随时间变化与网格数量的关系图。如图2所示，网格数在86 w以上时基本不会对模拟结果产生影响，为保证模拟精度并确保求解时间，本文采用86 w网格数作为模型的基准网格数进行模拟。从图中也可以看出，数值模拟结果与参考文献中的实验结果趋于一致，说明本文采用的模型可以用于研究液滴撞击球面的Leidenfrost现象。

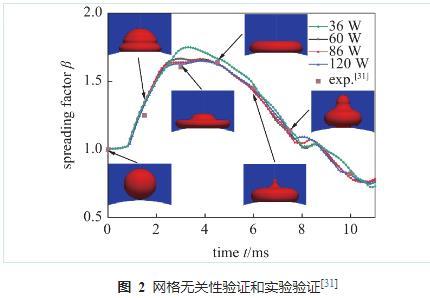
图2网格无关性验证和实验验证

图3进一步给出了不同时刻液滴撞击球面的形态变化，图3（a）为二维模拟结果、图3（b）为文献的实验结果、图3 c为paraview处理后的三维化模拟结果。如图所示，0 ms时刻，液滴以0.348 m/s的速度撞击球面，随后液滴由惯性力驱动开始铺展，铺展过程中动能不断转化为表面能和耗散能。1.5 ms-4.5 ms时段，液滴由球状逐渐转变为圆盘状。达到最大铺展系数后，表面张力促使液滴回缩，6.0 ms-7.5 ms时段，液滴逐渐回缩并开始反弹，上下部分出现较明显分界，整体呈葫芦状。10.0 ms时，液滴与壁面的接触面积明显减少。15.0 ms时，液滴与壁面完全分离。可以看出，模拟结果与实验情况吻合良好，进一步证明本文数值模拟的准确性。

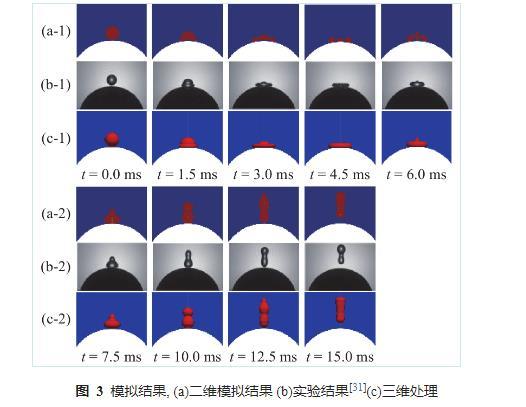
图3模拟结果，（a）二维模拟结果（b）实验结果（c）三维处理