毛细作用的尺度在微米到毫米之间，其所处的尺度是连接宏观与微观的桥梁。表面张力不但与表面化学性质（分子层次）有关，还与宏观的现象，比如毛细浸润，毛细上升等现象有关。从分子层次上去理解表面能，表面张力的概念，对界面的微观认识具有重要的意义。

下面我们从分子论的角度来认识表面自由能。

表面自由能定义为“将本体沿某一界面分开克服本体内分子间内聚引力的作用所需要做的可逆功”。这种克服内聚引力所做的功以势能的形式储存在新产生的表面上，就是表面自由能。

按照分子理论，两个分子间存在Van der Waals力，对应存在两分子间的van der Waals相互作用势，其表达式为

式中，Cvdw为Van der Waals分子对作用势系数，且

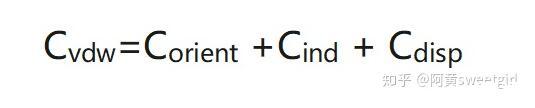
其中，Corient为Kessom分子对取向作用势系数，Cind为Debye分子对诱导作用势系数，Cdisp为London分子对色散作用势系数。为分子方便，把原公式中负号去掉，即把吸引作用是为正。

而两分子间的Van der Waals力的大小和表示为：

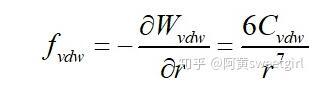
其方向沿两分子的连线方向。

对于物体系统来说，按照Hamaker理论，物体系统的总作用势等于各个分子间互相作用势的叠加，即

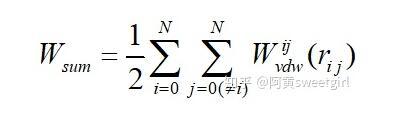
式中Wij是分子i和分子j间的不受其他分子影响的互作用势；rij是分子i和分子j间的距离；N为总分子数。

根据这一原理，单个分子与有限厚无限大平板的互作用势为

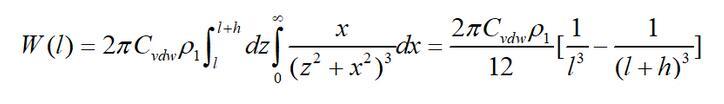
始终ρ1为无限大平板物体单位体积的分子数（分子密度）；h为平板的厚度；l为单个分子到平板的最近距离。

当厚度取无限大时可得单个分子与半无限体间的互作用势为

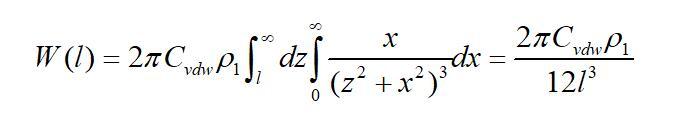
将单个分子换成有限厚无限大平板的单位面积，可得有限厚无限大平板之间的互作用势为

式子中h1和h2分别为两无限大平板的厚度。

当h1趋近于无穷时，得有限厚无限大平板与半无限体的互作用势为

当h1和h2都趋近于无穷时，得两半无限体之间的互作用势为

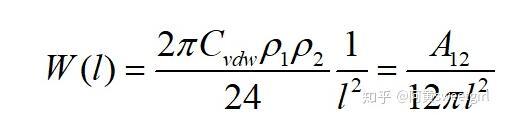
式中A12为Hamaker常数。定义为：

若取l为物质本体内分子间的距离d11，且两半无限体为同一种物质时，则上式的互作用势变为（取绝对值

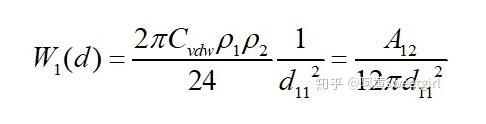
式中，

为物质1的Hamaker常数。该作用势能就相当于本体的内聚功。从表面自由能的定义不难看出，当将本体沿本体内的一个界面分开时，单位面积需要克服内聚力所做的功就等于这个作用势能。由于分开后形成两个新表面，因此每个表面上的势能等于该势能的一半。因此物体的表面自由能（表面张力）也等于该作用势能的一半，即

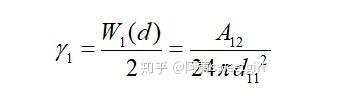
同样，若取l为两相界面处分子间的距离d12，且两半无限体为两种不同的物质时，则互作用势变为

该作用势能就相当于两相之间的粘附功。由于粘附功与表面张力（自由能）和界面张力（自由能）有如下关系：

式中γ12为界面张力（自由能）。则界面张力/自由能可表示为：

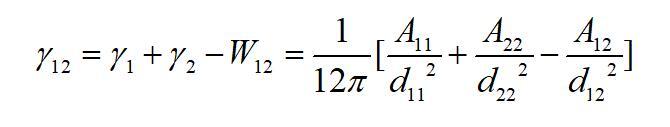
式中d11为物质1的分子间距；d22为物质2的分子间距；d12为物质1和物质2在界面处的分子间距；A11、A22及A12分别为物质1本体内、物质2本体内及物质1与物质2之间的Hamaker常数。

参考：节选自《毛细力学》第三章，高世桥，刘海鹏，科学出版社，2010.