合作客户/
拜耳公司 |
同济大学 |
联合大学 |
美国保洁 |
美国强生 |
瑞士罗氏 |
相关新闻Info
-
> 表面张力测量科学:从经典原理到现代智能操作(以Kibron表面张力仪为例)
> 中性聚合物键合剂(NPBA)与奥克托今(HMX)界面张力测定及应用效果(一)
> 覆盖有疏水网的开放管道液体输运稳定性研究(上)
> 各种表面活性剂性能一览表
> 不同浓度下甘草酸溶液界面张力的变化
> 肺内液表面张力的作用、临床意义及测量方法(一)
> 新型POSS基杂化泡沫稳定剂表面张力测定及对泡沫压缩性能的影响(一)
> 不同相对两亲面积的Janus颗粒在油气表面性质和泡沫性能对比(二)
> 中性聚合物键合剂(NPBA)与奥克托今(HMX)界面张力测定及应用效果(三)
> 软物质褶皱形成机制新发现:液体浸润、表面张力与接触线钉扎效应
推荐新闻Info
-
> 烷基糖苷表面活性剂界面张力与润湿性相关性研究(二)
> 烷基糖苷表面活性剂界面张力与润湿性相关性研究(一)
> 嵌段比例对温敏聚合物表面张力的影响及临界胶束浓度分析(五)
> 嵌段比例对温敏聚合物表面张力的影响及临界胶束浓度分析(四)
> 利用表面张力优化浮选工艺:调整剂AY在石英-胶磷矿分离中的活性调控(二)
> 利用表面张力优化浮选工艺:调整剂AY在石英-胶磷矿分离中的活性调控(一)
> 嵌段比例对温敏聚合物表面张力的影响及临界胶束浓度分析(三)
> 嵌段比例对温敏聚合物表面张力的影响及临界胶束浓度分析(二)
> 嵌段比例对温敏聚合物表面张力的影响及临界胶束浓度分析(一)
> 温度和碳碳双键数对脂肪酸酯表面张力的影响(二)
气泡液体中的演变动力学分析
来源:知乎 阿黄sweetgirl 浏览 2004 次 发布时间:2021-08-21
气泡液体是大小不同的球状气泡分散到液体中的液气体系。在气泡液体中,大小不同气泡是一个不稳定的体系,其内部不等的压强会使整个体系变化,总体趋势是气泡半径出现粗化现象,这种粗化跟晶体生长中的Ostwald熟化的现象是一致的(Ref 1)。根据附加压力公式,可知较小的气泡其内部具有较大的压强,因此与旁边较大的气泡间就会存在压强差(图1a),气泡间液体两侧的压强差会使气体从压强较大的地方向较小的地方扩散,从而出现大的气泡增大,小的气泡减小直至消失的情形,这就是气泡Ostwald熟化的机理(Ref 2)。从能量的观点来说,Ostwald熟化的结果降低了体系的表面能,从而使整个体系更加稳定。

图1(a)气泡演变Ostwald熟化原理(b)Lemlich理论中半径为ρ的假想气泡模型
从定性的角度来看,气泡的Ostwald熟化的过程是大气泡吸收小气泡的过程。但从定量上的角度来说,在气泡演变的任一时刻,到底尺寸为多少的气泡倾向为长大,而尺寸为多少的气泡减小而倾向于消失呢?1978年,美国辛那提大学的Robert Lemlich建立模型解决了这个问题(Ref 3)。Lemlich的理论核心和依据是:1)假设所有的气泡内的液体相互扩散时,都是先把气体扩散到液体中,再通过液体扩散到其他气泡中实现Ostwald熟化过程(图1a),这个假设在气泡含量不高,不是相互接触的情形下是合理的。2)在气泡演化的任何一个时刻,液体中气体的浓度是均匀一致的,这个假设在研究所有气泡的演化整体行为上是可行的。3)依据亨利定律,这个液体中气体的浓度可以等价为液体内部有一个气体压强,而这个压强可以看成是一个假想的气泡内部的压强(图1b),其半径ρ可以依据Laplace方程计算出来。所以,所谓气泡演化就是所有气泡跟这个假想的气泡进行气体交流。这样就把体系中气泡演变多对多扩散的复杂情形简化为了多对一的演变过程。由此,体系中任意一个半径为r气泡与这个液体的中假想的气泡的压强差△P为

公式1
此气泡与液体(假想气泡)之间的气体的以摩尔为单位的传输速率Qm为

公式2
公式中J为气体的有效渗透系数,As为气泡气体传输发生的表面积,dn/dt是单位时间传输的摩尔数。对于球形气泡As=4πr^2,在任一时刻,通过所有气泡界面的气体量是守恒的,即
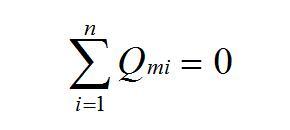
公式3
假设气体符合气体理想气体方程,即PV=nRT,对于球形气泡,体积V=4πr^3/3,从而可把摩尔速率转化为气泡半径变化的速率。通过以上各式,可得
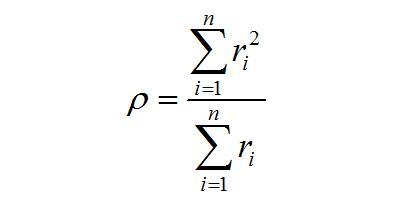
公式4
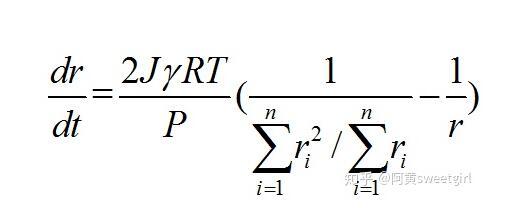
公式5
这就给出了气泡Ostwald的动力学方程。对于任意气泡体系,知道某时刻的气泡体积或者半径分布,就可以利用公式4算出ρ判定体系中的气泡是增大还是减小,气泡半径大于ρ的在这一时刻又增大的趋势,小于的会在下一时刻减小,根据ρ的公式,其含义是所有气泡的瞬时平均半径。而且,利用公式5就可以预测气泡在后面任意时刻的气泡分布,以及气泡的演化的最终状态及所需要的时间。
Lemlich的理论在预测低含量的气泡时的演化规律无疑是合理而准确的。而且气泡含量越低,其准确性越高。最重要的原因他的理论建立在气体传输发生在气泡与液体而不是气泡与气泡之间。对于高浓度的气泡液体,气泡之间相互挤压,气体传输可以直接通过气泡接触的边界进行。而且在演化中,液体的局域气体浓度也不全相同,在预测这类演化时,会出现较大的误差,需要用到泡沫的结构与演化规律去解释。
笔者借用这种理论,讨论了在微结构下气泡的演变行为。并去控制气泡的演变过程和演变方向,其相应结果发表在Ref4中。控制演变过程的动画如下所示:

微结构下气泡演变的集聚效应
即刚开始无序的气泡,在生长和微结构的调控下,最终全部演变为正十二边形的规则气泡阵列。
Ref 1:Lifshitz,I.M.&Slyozov,V.V.The Kinetics Of Precipitation From Supersaturated Solid Solutions.J.Phys.Chem.Solids 19,35-50(1961).
Ref 2:Stevenson,P.Inter-bubble gas diffusion in liquid foam.Curr.Opin.Colloid Interface Sci.15,374-381(2010).
Ref 3:Lemlich,R.Prediction of Changes in Bubble Size Distribution Due to Interbubble Gas Diffusion in Foam.Ind.Eng.Chem.Fundam.17,89-93(1978).
Ref 4:Zhandong Huang,Meng Su,Qiang Yang,Zheng Li,Shuoran Chen,Yifan Li,Xue Zhou,Fengyu Li,Yanlin Song*.A general patterning approach by manipulating the evolution of two-dimensional liquid foams.Nat.Commun.2017,8,14110.
注:此文摘选自本人博士毕业论文。










