合作客户/
拜耳公司 |
同济大学 |
联合大学 |
美国保洁 |
美国强生 |
瑞士罗氏 |
相关新闻Info
推荐新闻Info
-
> 我第一次操作表面张力仪的心得体会
> pH对马来松香MPA与纳米Al2O3颗粒形成的Pickering乳液类型、表/界面张力影响(四)
> pH对马来松香MPA与纳米Al2O3颗粒形成的Pickering乳液类型、表/界面张力影响(三)
> pH对马来松香MPA与纳米Al2O3颗粒形成的Pickering乳液类型、表/界面张力影响(二)
> pH对马来松香MPA与纳米Al2O3颗粒形成的Pickering乳液类型、表/界面张力影响(一)
> 基于药液表面张力测定估算苹果树最大施药液量的方法(四)
> 基于药液表面张力测定估算苹果树最大施药液量的方法(三)
> 基于药液表面张力测定估算苹果树最大施药液量的方法(二)
> 基于药液表面张力测定估算苹果树最大施药液量的方法(一)
> 矿用尘克(C&C)系列除尘剂对大采高工作面截割煤尘的降尘效率影响(三)
激光深熔焊接表面皱纹组织的产生原因及表面张力计算公式
来源:激光制造(解读) 浏览 711 次 发布时间:2024-06-26
极窄小孔的稳定性仍然是20kW或更高级别激光焊接的最大挑战。本文研究了小孔失稳的根本原因,包括褶皱结构引起的热失稳和蒸汽引起的动态失稳。建立了多相流模型,结合高效的自由表面重构算法和高精度的皱纹面结构观测平台,研究了极窄小孔表面的形态演化和热力学行为。研究发现,小孔前壁上存在的褶皱结构(驼峰)可以显著调节小孔的能量分布,改变小孔的受力状况。驼峰分布异常引起的能量积累过大是导致小孔孔壁波动不稳定的原因。通过提高焊接速度,抑制了激光与小孔开口之间的间歇接触行为,从而有助于减少驼峰的产生。通过增大激光功率,避免了固-液界面的打孔效应,提高了小孔前壁熔化层的向下流动效率。提出了一种基于焊接速度和激光功率调节的皱纹控制优化策略。实验结果表明,优化后的皱纹面结构显著提高了小孔的稳定性。
方法
实验采用的是连续波光纤激光器(IPG YLS-30000),其光束参数为:最大激光功率30kW,波长∼1070 nm,纤芯600mrad m,光头F180/F470,瑞利长度31.47 mm,光束参数乘积22.8 mm×μ。工艺参数如表1所示。母材为30 mm厚的SU316L钢板。化学成分如表2所示。焊接前,钢板用丙酮溶液清洗,以去除氧化膜和油脂。采用气体保护气体侧向供气,流量1.5m~3/h,将透明石英玻璃(GG17)与现场观察的焊接试件对接。激光光斑位于对接接头上,偏向不锈钢,以避免玻璃软化。从光束中心到对接的距离为光斑半径的1/2。使用5000fps(每秒帧)的高速相机(Phantom V611)观察小孔和熔池轮廓。使用最大功率为30W的半导体激光器(808 Nm)照射观察区。在相机镜头上组装了一个透射带为808 nm的带通滤光片,以滤除周围的光线。
为了研究激光深熔焊接过程中表面皱纹组织的产生和蒸汽压的波动,建立了多相(固、液、气/气)模型。在该模型中,提出了一种基于三线性插值法的快速自由曲面重建方法(TRI-MC)[21],用于计算皱纹结构的几何信息。对激光反射、局部蒸发、熔池流动和小孔动力学进行了直接模拟。为了降低计算成本,对以下过程进行了简化:假设小孔附近的流体流动为层流、不可压缩和牛顿流动;焊接过程中忽略了保护气体的冲击。
表面张力的计算公式为:
ϒm是纯金属在熔点Tm的表面张力,A是纯金属的dϒ/dt的负值,R是气体常数,S是饱和时的表面过剩,Kseg是平衡分凝系数,H0是标准吸附热,H‘Mi是偏摩尔能,Ki是与分凝熵有关的常数。
图1(A)中显示了计算领域的图形说明。计算域的大小设置为20 mm×2 mm×25 mm。计算域划分为1.25亿个边长为0.02 mm的六面体网格。在初始状态下,将厚度为20 mm的下部设置为工件层(阶段2),将厚度为5 mm的上部设置为环境空气层(阶段1)。前壁(Y=0)被设置为对称边界条件,顶面(Z=25 mm)被设置为压力输出边界条件,其他表面被定义为壁边界条件。使用了Ansys-FLUENT®软件用于模拟。采用C语言编写的用户自定义函数(UDF)实现光线跟踪过程。图1(B)显示了光线追踪过程的验证案例,在该案例中,一束平行光束被射入具有不同表面粗糙度的方腔。图1(C)表明,在高Ra条件下,随着表面粗糙度的变化,能量分布明显改变,更多的能量集中在第一反射区。表3列出了模拟中使用的物理特性。
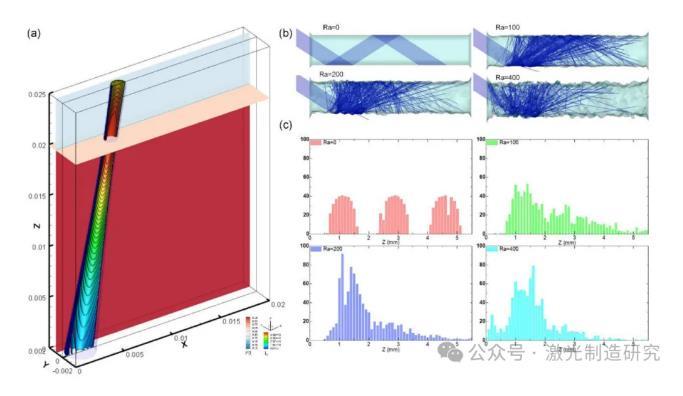
图1.(A)计算区域和高斯热源分布示意图;(B)不同表面粗糙度下激光光线追踪模型的验证;(C)不同表面粗糙度下的反射点分布。
主要结论
(1)根据钥匙孔半径(r)和局部蒸汽喷射流特征长度(lv)的比值,后钥匙孔壁可能受到两种支撑力的支撑。当r/lv<1时,钥匙孔受蒸汽喷射压力的作用,保持在动态稳定状态。当r/lv>1时,锁孔受蒸汽静压的作用,处于临界稳定状态。在动态稳定状态下,匙孔具有更强的抗干扰能力(匙孔半径波动)。通过将吸收的激光强度调整到0.2至0.5 MW/cm2的范围内,可将锁孔控制在动态稳定状态。
(2)能量吸收率与钥匙孔前壁驼峰的几何形状密切相关。随着驼峰尺寸的增大,吸收的激光强度可能会在几个驼峰上过度集中(>0.5 MW/cm2),从而导致匙孔剧烈波动。抑制大尺寸驼峰的产生是调节能量分布、提高焊接过程稳定性的主要手段。
(3)驼峰是在激光束与钥匙孔开口间歇接触时产生的。当焊接速度高于蒸发速度(vc≥vp)时,驼峰可被完全抑制。但在焊接速度较低(vc<2 m/min)时,驼峰则无法完全避免。
(4)当熔体向下流动受阻时,驼峰尺寸会迅速增大,固液界面上存在的阶梯状平台是熔体受阻的原因。提高激光功率有助于改善熔化层的向下流动,减少固液界面的热传导(熔化层钻孔效应)。因此,驼峰的尺寸可以限制在可接受的范围内。










