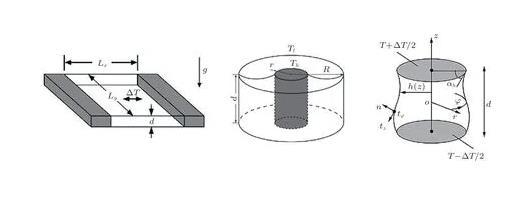
液层模型是源自于空间晶体生长实验探索的简化模型，是研究微重力条件下界面张力梯度驱动对流基本流动规律的经典模型。液层模型主要包括矩形液层（rectangular pool）、环形液层（annular pool）和液桥（liquid bridge）（图1）等。相对而言，液桥是一类特殊的液层模型。液桥中界面张力梯度驱动对流的流动稳定性研究成果极为丰富，相关系统的完整临界转捩描述详见综述（Hu et al.2008）。除了极薄液层的情况，在绝大多数界面张力梯度驱动对流的地面实验研究中，界面张力效应和重力效应间存在较强的耦合作用。

例如，Riley和Neitzel（1998）的地面实验研究结果表明，液层中热流体波的特征，如传播角度和振荡频率，随着液层厚度的不同而改变，表现出与重力效应的强耦合性。这与Chan和Chen（2010）的研究结论一致。而另一方面，由于空间实验机会昂贵稀缺，界面张力梯度驱动对流的空间实验研究屈指可数。Kamotani等（1995,1999）开展了圆形液池中界面张力梯度驱动对流临界转捩的空间实验研究，实验采用的液层厚度相对较厚，高径比约为1.实验研究了层流失稳的临界条件和临界流动振荡模式，讨论了其与加热速率、自由面位形和激光束加热面积的关系，并和相应的数值模拟结果进行了比较。环形液层的特点是周向没有壁面限制，热流体波不会因为壁面影响而衰减（Lappa 2009），可以更好地观测热流体波的基本参数，例如临界波数的变化。Schwabe等（1999,2002）开展了外加热环形浅液池中界面张力梯度驱动对流的临界转捩空间实验研究。

实验结果表明临界值与液层尺度比无关；实验中还确认了热流体波的存在，当液层高度很小时，随Marangoni数的增加，流动由同心多卷圈结构发展为热流体波；而当液层厚度较大时，失稳后的流动比热流体波更为复杂和不规则；此外，实验中还发现特殊的轴对称临界振荡。但是实验结果分析中没有考虑自由面位形的影响，部分实验结果与二维矩形液层的数值模拟结果有较大差别。近期，Jiang（2017a,2017b）通过实验研究了矩形液层热毛细对流的转捩问题，发现了多种转捩途径，并发现存在表面波动不稳定性。Kang等（2019a,2019b,2019）在实践10号返回式科学卫星上开展了内加热环形液池中界面张力梯度驱动对流的临界转捩空间实验研究，实验结果给出了层流失稳的临界条件，

临界振荡流动模式及振荡频率等，系统讨论了上述临界转捩特征与液层体积比（自由面位形）关系。这里液层体积比定义为液层实际体积与对应的水平液层的体积之比。此外，Kang等（2019d,2020）在天宫二号（TG-2）空间实验完成了液桥热毛细对流空间实验，讨论液桥高径比–体积比的几何参数效应、多次转捩、波动模式变换、以及分岔道路的复杂性。

相比有限的空间实验结果，微重力条件下界面张力梯度驱动对流临界转捩的理论和数值模拟研究的成果更为丰富。Pearson（1958）重新分析了B´enard（1901）的实验，通过在边界条件中加入界面张力项，动量方程中忽略重力项，建立了纯界面张力梯度作用下的数学物理模型，由理论分析给出了流动由静止状态到形成胞状对流的临界条件，与B´enard的实验结果较为符合。Pearson的研究开启了一系列对于液层界面张力梯度驱动对流的研究。Smith和Davis（1983）利用线性稳定性方法研究了微重力条件下无限长的液层，其自由面上施加均匀温度梯度，研究发现，在自由面不变形假定下，除了Pearson指出的定常卷圈结构外还有热流体波的失稳形式；当考虑自由面变形时，表面波不稳定性的形式是行波。相关临界值、传播方向和临界波数等受流体物性和界面传热的影响。

此外，实际液层的有限边界对热流体波传播有明显限制，进而影响其稳定性。Xu和Davis（1984）研究了轴向施加均匀温度梯度的无限长流体圆柱，同样发现了与轴向成一定角度传播的热流体波。Smith和Davis（1983,1986）对热流体波不稳定性的物理机理进行了讨论，指出热流体波是一种与热效应相关的波动，流场主要起对流输运的作用，即使在忽略表面变形时也会产生热流体波。另一种表面波不稳定性则是表面波动变形与内部剪切流动耦合作用的结果，是纯粹的流体动力学效应。Derby和Brown（1986）最早在微重力科学计划支持下利用环形液层模型开展了提拉法空间晶体生长的模型化研究。Laure等（1990）通过线性稳定性理论和局部分岔理论分析了矩形液池界面张力梯度驱动对流的扰动的空间分布等问题。

Xu和Zebib（1998）对大Prandtl数界面张力梯度驱动对流进行了二维和三维数值模拟，对于二维模型，研究给出了较为完整的不同Prandtl数与高径比下流动失稳的临界Reynolds数（Re=γ∆TH/µν,其中γ=−∂σ/∂T,H为特征长度），并从能量角度分析了振荡流产生的机制；对三维模型，研究给出了典型的Prandtl数下不同高径比时流动失稳的临界Reynolds数；同时，研究指出侧壁可以起到抑制失稳的作用，而第三个维度方向上的扰动则会促进失稳。Madruga等（2003,2004）对两层流体在水平温差作用下的界面张力梯度驱动对流进行了线性稳定性分析，发现了三种不稳定形式：从冷端向热端传播的行波、从热端向冷端传播的行波，以及纵向卷圈。P´erezgarc´ıa等（2004）理论分析了硅油液层厚度对界面张力梯度驱动对流线性稳定性的影响，指出对流会从基本流失稳为热流体波或者纵向涡胞，是由不同的液层厚度所决定的。

Li等（2011a,2011b）采用渐近分析方法研究了单层和双层环形液层内的定常轴对称界面张力梯度驱动对流。Shi等（2006,2010）开展了环形浅液层界面张力梯度驱动对流的线性稳定性研究，分析了浮力效应、旋转等对稳定性的影响，研究表明，随着Marangoni数增加，流动由单一传播方向和波数的热流体波发展为各种传播方向和波数的热流体波的叠加状态。Sim等（2003,2004）采用三维直接数值模拟方法研究了环形液层内界面张力梯度驱动对流从定常轴对称到三维流动的转捩，发现了在不同尺度比（厚度与半径之比）下，液层失稳后出现沿周向的行波和驻波，并研究了界面换热的影响。Li等（2003,2004）对不同深度外加热环形浅液层中的小Prandtl数热毛细对流和浮力–热毛细对流进行了三维数值模拟，考虑了底面绝热和底面恒定热流的情况，研究发现表面温度场呈现的不同振荡形式：周向传播的热流体波、受到径向扰动调制的热流体波、驻波等。

石万元等（2009）发现环形浅液池临界转捩后形成对数螺线形波纹的热流体波，相应传播角为常数并随着驱动力增加而增大。Tang和Hu（2007）数值模拟研究微重力环境下矩形浅液池内的热流体波，对热流体波的形成机理进行了分析和讨论。胡文瑞等（2010）对矩形液池中的界面张力梯度驱动对流起振过程进行了数值模拟，发现微重力条件下液池两侧的温差超过临界温差时，液池中就会出现振荡对流，其涨落值远小于时间平均值，表现为从冷端向热端传播的热流体波。

Li等（2012）对微重力环境下Marangoni对流和热毛细对流耦合的液层进行了数值模拟，预测了耦合对流的多涡流结构和临界稳定边界，并报道了振荡耦合对流。Ma和Bothe（2011）采用基于VOF方法的直接数值模拟方法研究了动态自由面形变对液层界面张力梯度驱动对流的影响。S´aenz等（2013）研究了浅矩形液池内界面张力驱动对流热流体波及其动态自由面形变对不稳定性的影响。

值得指出的是前述对于界面张力梯度驱动对流临界转捩的理论和数值模拟研究大多针对水平自由面模型开展。空间环境下自由面的形状通常是弯曲的，自由面位形对于界面张力梯度驱动对流及其稳定性有重要的影响（Garnier&Normand 2001,Ma&Bothe 2011,Saenz et al.2013）。从流体力学基础研究和空间应用两方面来说，开展弯曲自由面液层体积效应对流体流动的临界转捩特征的影响的研究都是非常必要的。