合作客户/
拜耳公司 |
同济大学 |
联合大学 |
美国保洁 |
美国强生 |
瑞士罗氏 |
相关新闻Info
推荐新闻Info
-
> GA、WPI和T80复合乳液体系的脂肪消化动力学曲线、界面张力变化(四)
> GA、WPI和T80复合乳液体系的脂肪消化动力学曲线、界面张力变化(三)
> GA、WPI和T80复合乳液体系的脂肪消化动力学曲线、界面张力变化(二)
> GA、WPI和T80复合乳液体系的脂肪消化动力学曲线、界面张力变化(一)
> 表面张力实验、接触角实验分析抑尘试剂对煤的润湿结果
> Kibron表面张力仪研究烧结矿聚结行为
> 基于界面张力和表面张力测试评估商用UV油墨对不同承印纸张的表面浸润性差异(三)
> 基于界面张力和表面张力测试评估商用UV油墨对不同承印纸张的表面浸润性差异(二)
> 基于界面张力和表面张力测试评估商用UV油墨对不同承印纸张的表面浸润性差异(一)
> 分子动力学模拟不同浓度仿生黏液-水界面的界面张力
水滴的表面张力使它尽量收缩从而形成球形
来源:知乎 贾明子 浏览 2749 次 发布时间:2021-06-21
从高处往下倒水,为什么刚开始水是连成一条线的,往下就成了散开的水珠?有什么方法能让水一直保持一条线?
先说结论,这是因为所谓的“Plateau–Rayleigh”不稳定性。
然后,我再试图用大家都能听懂的白话解释一下。这个过程中有一个关键的物理现象,叫做表面张力。
表面张力,我们简单形象地理解,可以认为流体的两相(如气液)界面就像是一张紧绷的皮膜,这张膜在外力的约束下,总是希望尽可能地收缩。沿着它的表面就有一种张力,就是表面张力。
如果你想用最形象的方式理解表面张力,你可以想象一个吹起来的气球的表面:气球的弹力使它尽量收缩从而整体形成球形。相对应地,水滴的表面张力使它尽量收缩从而形成球形。

而这里有一件非常关键的事请,就是由于表面张力的存在,弯曲的表面就会在两侧形成压力差。就好像紧绷的气球,其内部压力要高于外部的压力。这种压力差来自哪里?当然就是气球皮膜紧绷的张力。由于气球的弯曲表面,使得其张力最终表现为内部压力的升高。
具体讲,我们对一个这样无重力液滴做出分析,它的上半球受力受到三个力的作用:
1、内部液体在截面上对它的净压力;
2、外部在上半球面上对它的净压力
3、液滴表面受到的沿表面垂直于“断面”的表面张力。
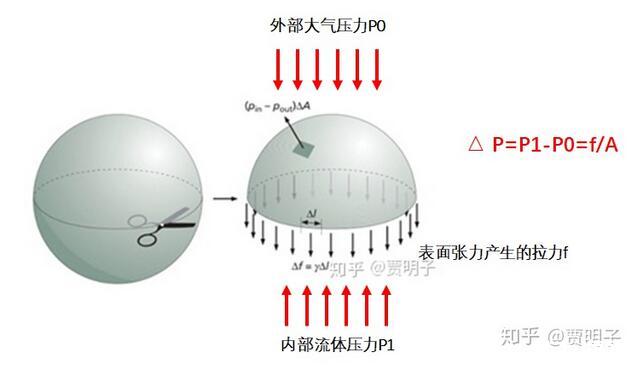
我们很容易就会看到,由于表面张力的存在,此时内部的压力肯定要大于外部压力。那么,这种压力差的大小是由什么决定的呢?
很显然,一个决定因素就是张力的大小:皮膜绷的越紧,所能产生的压力差就越大。但是还有另一个很重要的因素,就是表面弯曲的程度,也就是它的曲率。我们还是用气球做一个说明,例如下面这个气球:

气球内部的气体压力处处相等,但是,接触过这种气球的人都有一个经验,就是粗的地方绷得紧,而细的地方绷得就不那么紧。如上图所示,绷得紧的地方和绷得松的地方,产生的压力差是相等的,但是他们的曲率是不相等的:曲率越大,同样的张力所能产生的压力差就更大。
我们有一个公式可以表示这个关系,叫做杨-拉普拉斯方程(Young-Laplace equation):
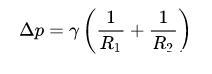
其中,γ是表面张力,R1和R2分别是两个方向上的曲率半径。
那么,我们来看看细流的水柱为何会分散成水滴:这是因为连续的水柱状态是不稳定的,而水滴的状态才是稳定的。比如说,下图是一个细流柱:
我们知道,我们的环境中总是存在着各种干扰,不论我们如何隔离,都不可能消除它:因为水柱自身就存在各种涨落。因此,这个水柱不可能是严格的圆柱形,它上面总是有各种“皱纹”的。事实上,现实中的扰动非常之复杂,我们不可能做出具体的分析,但是,我们总是可以把这些扰动看做是一系列正弦波的叠加(傅里叶分解),那么,我们通过对这些正弦波的分析,可以分析出这些干扰的基本特征。如下图,一个被正弦波干扰的水柱呈这个形状:
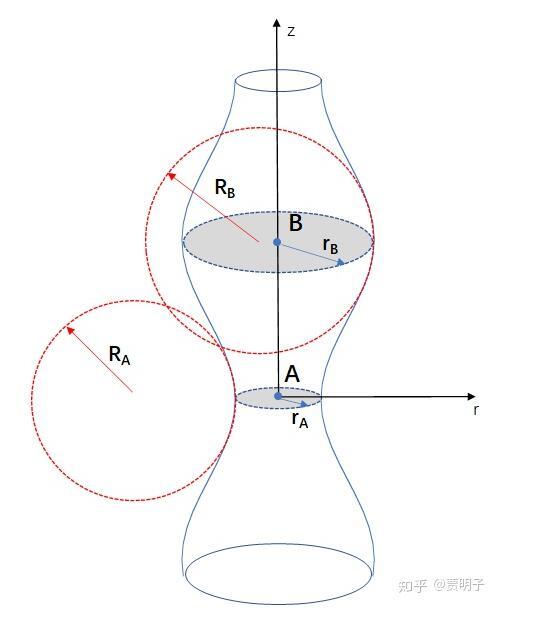
我们可以看到,在不同的地方,柱面的曲率都发生了变化,这种变化和表面张力一起,就导致了水柱当中不同地方内部压力的变化。那么,我们如何判断这种影响呢?我们说,如果A点(柱半径缩小的地方)的压力上升,B点压力下降,那么:
在压力差下,流体从A点流向B点,
流动导致A点进一步缩小,B点进一步增大
进而,A点压力更加增加,B点的压力更加减小
流动更加快速
……
如此循环,A点处迅速缩成0,从而崩解,也就是说,这是一种正反馈,表面张力的作用会扩大扰动,水柱不复存在。
但是,如果发生的情况相反,也就是说,扰动导致B点压力上升,A点压力下降,那么,水就会从B点流向A点,这是一种负反馈,表面张力的作用会抑制扰动,水柱就能维持稳定。
那么,这种扰动到底会是一种正反馈,还是负反馈呢?我们来具体分析两点的压力变化:
在A点,z方向上产生了负曲率(半径RA),而r方向上,由于半径变小,曲率变大。也就是说,A点上的曲率变化产生了两个效果:
柱面的正弦波导致负曲率,使得A点的压力下降;
截面的半径变小,导致A点压力上升。
同理,我们也可以看到,在B点,两个效应是相反的:
柱面正弦波导致正曲率,使得B点压力上升;
截面半径增大,导致B点压力下降。
也就是说,扰动导致的z方向上的正弦波曲率将会升高B点压力,降低A点压力,导致负反馈,水柱稳定;而扰动导致水柱粗细的变化,将会升高A点压力,降低B点压力,导致正反馈,水柱崩解。
从直观上我们立刻就知道,如果水柱很细,那么截面上的曲率很大,它的影响会显著大于正弦波的影响,那么就会是正反馈,水柱崩解;反之,如果水柱很粗,那么截面上曲率很小,起到关键作用的将会是正弦波造成的曲率,那么就会是负反馈,水柱稳定。
这就是为何细水柱不稳定的原因。
那么,水柱到底多细,才会不稳定呢?下面我们来简单计算一下:
假定扰动所导致正弦波的形式如下:
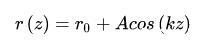
这里,是未受到扰动的水柱半径,A表征扰动的大小,而k是波数,表示扰动范围的大小。很容易,我们可以计算出两个方向的曲率半径,进而根据Young-Laplace方程计算出流体内部各处的压力(我们假定外压为零):
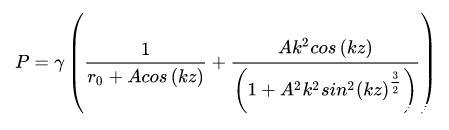
在A点,,在B点,,那么,我们可以得到:
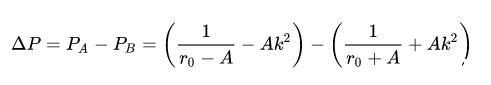
这就是扰动导致AB两点的压力差。根据上面的讨论,当它小于0的时候,水柱就是稳定的,也就是说:
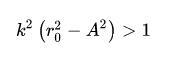
请注意,理论上,当水柱稳定的时候,它是可以抗拒任意小的扰动的,也就是说,在我们取的极限时,水柱仍然稳定。所以说,我们就得到了水柱稳定的条件如下:
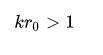
从这个条件看,水柱的半径越细,就越难满足稳定条件,进而它就更容易崩解。
而在水向下自由流动的过程中,由于重力作用,它是在加速的,也就是说,越往下它流动速度越快,自然就会导致其越往下水柱越细:
所以,这就回答了题主的问题:
从高处往下倒水,为什么刚开始水是连成一条线,往下就成了散开的水珠?










