合作客户/
拜耳公司 |
同济大学 |
联合大学 |
美国保洁 |
美国强生 |
瑞士罗氏 |
相关新闻Info
-
> 湿润剂的表面张力大小对硫化矿尘湿润效果和湿润行为的影响
> 什么叫熔体,表面张力对陶瓷熔体的作用机理
> 10种常用表面活性剂水溶液的表面张力测定、泡沫的产生和测试(一)
> 酚胺树脂聚醚型破乳剂分子结构、浓度对油-水界面张力的影响——结果与讨论、结论
> 一种新表面张力改性方法让全固态电池性能更优
> 氧化石墨烯纳米流体的凝固特性及在声悬浮下表面张力研究
> 接触角迟滞时气~液界面张力的温度敏感性对液滴蒸发过程的影响——结果分析、结论
> 表面张力估算法测定29种常见低芳浅色矿物油的溶解度参数——结果与讨论、结论
> 新型十六烷基胺无碱表面活性剂的合成、界面性能及复配性能(二)
> 便携式表面张力仪和气泡压力法表面张力计介绍
推荐新闻Info
-
> 我第一次操作表面张力仪的心得体会
> pH对马来松香MPA与纳米Al2O3颗粒形成的Pickering乳液类型、表/界面张力影响(四)
> pH对马来松香MPA与纳米Al2O3颗粒形成的Pickering乳液类型、表/界面张力影响(三)
> pH对马来松香MPA与纳米Al2O3颗粒形成的Pickering乳液类型、表/界面张力影响(二)
> pH对马来松香MPA与纳米Al2O3颗粒形成的Pickering乳液类型、表/界面张力影响(一)
> 基于药液表面张力测定估算苹果树最大施药液量的方法(四)
> 基于药液表面张力测定估算苹果树最大施药液量的方法(三)
> 基于药液表面张力测定估算苹果树最大施药液量的方法(二)
> 基于药液表面张力测定估算苹果树最大施药液量的方法(一)
> 矿用尘克(C&C)系列除尘剂对大采高工作面截割煤尘的降尘效率影响(三)
一滴水缓慢落到非常光滑的平面上,接触面积会有多大?
来源:知乎 阿黄sweetgirl 浏览 2095 次 发布时间:2021-07-29
此问题中,其实绝对光滑不太合适,一般可以考虑原子级别的光滑就已经可以使用(或可以看做没有接触角滞后现象)。为了让解析式简便,此题转化为:
如果将体积为V的液体水滴落到原子级别光滑的光滑固体表面上,设固体表面对水的接触角为θ,那么液滴稳定后,液滴与固体之间的接触面积S有多大?
下面我仅仅使用参数V和θ,以及水的物性常数找出S的简单解析式。
首先,此题必须分为两种情形。第一种,是液体V很小时,此时表面张力占主导地位。此解法宫非前辈已经给出,但是其解析式不够简化。因此我进一步加以简化。当表面张力占主导时,液滴成完美的球缺状,如图1所示。
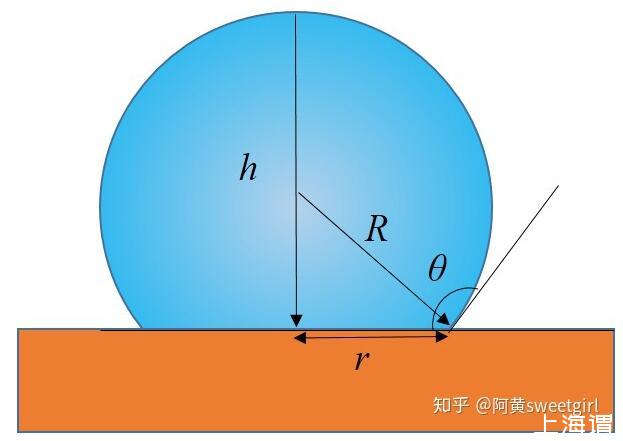
图1液体体积很小时,毛细作用力占主导的情形,液滴呈球形
此时根据球的体积公式,以及简单的三角函数变换,就可以得出S与V和θ的关系,具体推导过程如图2所示。
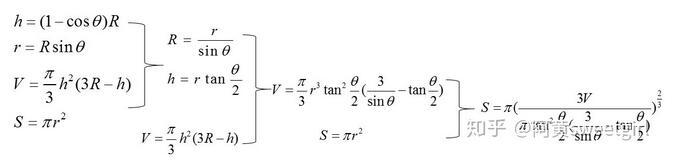
图2接触面积S的推导过程
此时可以看出,S与V的2/3次方是正比例关系。对于自然界任何光滑的表面,接触角处于0到122°的范围内,可以绘出S与θ的关系,如图3所示。
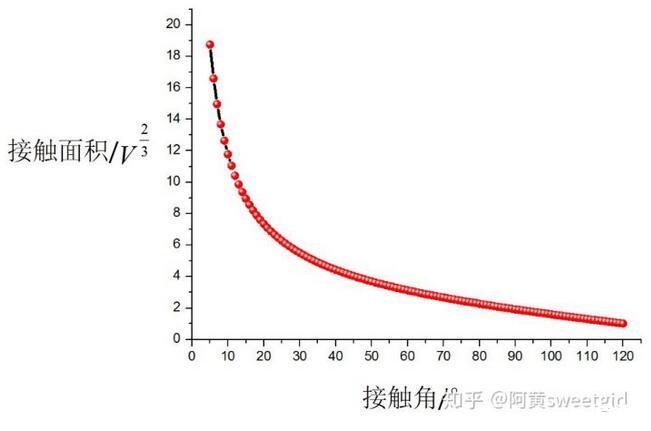
图3接触面积随着接触角的变化关系
上图是接触角从5°到120°范围内的接触面积的变化关系,基本上涵盖了自然界中的大多数物质的光滑固体表面。
然后再是第二种情形,就是液体体积很大,此时表面张力很弱,重力占主导地位的场景。此时,液滴在光滑固体表面的呈现出扁平状。如图4所示。

图4液体体积很大的情形
有意思的是,已经有前人对这种情形做过详细的受力分析。得出只要接触角一定,此时无论加多少水,液体的厚度e都不会增加,只会增加铺展的面积。其厚度e的表达式为:
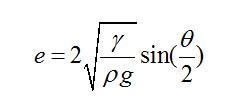
式中,γ为表面张力,p为密度,g为重力加速度。
由于此时,表面张力影响很小,液膜可以看成均匀的厚度,所以满足
V=Se
从而可以推出:
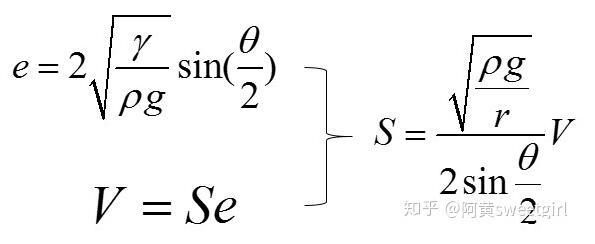
图5液体接触面积的推导公式。
至于具体的推导e的过程,可以见如下分析:


参考文献:Capillarity and Wetting Phenomena书籍。










